- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Carrier Transport Study Notes for Electronics and communication Engineering
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In this article, you will find the Study Notes on Carrier Transport which will cover the topics such as Introduction, Generation and Recombination Carrier Diffusion and Drift, Einstien Relation, Poisson’s Equation and Continuity Equation.
1. Introduction
- Any motion of free carriers in a semiconductor leads to a current. This motion can be caused by an electric field due to an externally applied voltage since the carriers are charged particles. We will refer to this transport mechanism as carrier drift. In addition, carriers also move from regions where the carrier density is high to regions where the carrier density is low. This carrier transport mechanism is due to the thermal energy and the associated random motion of the carriers. We will refer to this transport mechanism as carrier diffusion. The total current in a semiconductor equals the sum of the drift and the diffusion current.
- As one applies an electric field to a semiconductor, the electrostatic force causes the carriers to first accelerate and then reach a constant average velocity, v, due to collisions with impurities and lattice vibrations. The ratio of the velocity of the applied field is called mobility. The velocity saturates at high electric fields reaching the saturation velocity. Additional scattering occurs when carriers flow at the surface of a semiconductor, resulting in lower mobility due to the surface or interface scattering mechanisms.
- Diffusion of carriers is obtained by creating a carrier density gradient. Such gradient can be obtained by varying the doping density in a semiconductor or by applying a thermal gradient.
- Both carrier transport mechanisms are related since the same particles and scattering mechanisms are involved. This leads to a relationship between the mobility and the diffusion constant called the Einstein relation
2. Recombination
A process whereby electrons and holes are annihilated or destroyed.
Energy Bands in Recombination Processes
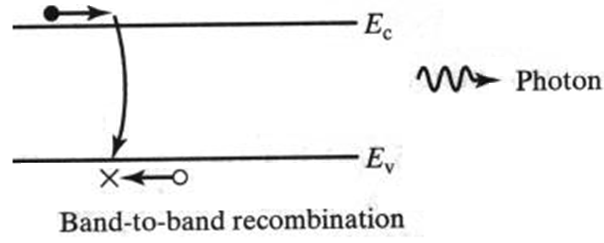
- Band-to-Band Recombination: Also referred to as direct thermal recombination, is the direct annihilation of a conduction band electron and a valence band hole. The electron falls from an allowed conduction band state into a vacant valence band state. This process is typically radiative with the excess energy released during the process going into the production of a photon (light).
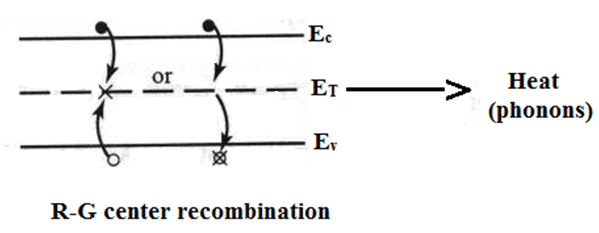
- R-G Center Recombination: A defect often causes an energy state in the mid-gap region of the bandgap that can act as traps for carriers. In this process, a conduction band electron gets trapped at this defect and energy state and then a valence band hole is trapped and recombines with the electron or vice versa. This process is typically nonradiative.
- Recombination via Shallow Levels: Donor and acceptor sites can also act as intermediaries in the recombination process similar to the R-G Center recombination with the exception that the recombination is quite often radiative.

- Recombination Involving Excitons: Conduction band electrons and valence band holes can form a slightly lower energy state by becoming bound to each other in a hydrogen-like arrangement. The electron and hole can then recombine and result in a photon that has energy slightly less than the bandgap.

- Auger Recombination: A nonradioactive recombination event where a conduction band electron loses energy to another conduction band electron which gains energy to result in one electron recombining with a hole in the valence band and one high energy electron which rapidly loses energy by phonon emission and relaxes back down to the conduction band.

3. Generation
A process whereby electrons and holes are created.
- The recombination processes can be reversed resulting in generation processes.
- Band-to-Band generation occurs when an electron from the valence band is excited by light or heat to the conduction band.

- Generation of an electron and hole by an R-G centre intermediary can be done in a couple of ways including an electron from the valence band being excited to the trap state and then to the conduction band creating a hole in the valence band and electron in the conduction band.

- Also, an electron in the trap state can be excited to the conduction band while the hole is excited to the valence band.

- Another common carrier generation is carrier generation via impact ionization where a high energy electron loses energy to produce an electron-hole pair.

4. Carrier Diffusion
- Diffusion: particle movement in response to concentration gradient
- Elements of diffusion:
- a medium (Si crystal)
- a gradient of particles (electrons and holes) inside the medium
- collisions between particles and medium send particles off in random directions: → overall, particle movement down the gradient.
Key diffusion relationship (Fick’s first law):
- Diffusion flux ∝ – concentration gradient
- Flux ≡ number of particles crossing unit area per unit time [cm−2 · s−1]
- For electrons:
- For holes:
- Dn ≡ electron diffusion coefficient [cm2/s]
- Dp ≡ hole diffusion coefficient [cm2/s]
- D measures the ease of carrier diffusion in response to a concentration gradient:
- Diffusion current density = charge × carrier flux
5. Carrier Drift
- Net velocity of the charged particles ⇒ electric current.
- Drift current density ∝ carrier drift velocity ∝ carrier concentration ∝ carrier charge.
- Drift currents:
- Total drift current:
- Has the shape of Ohm’s Law:
- Where:
- Then:
- Einstein’s Relation: In a semiconductor, this relation gives the relationship between diffusion constant, mobility and thermal voltage.
![]()
VT = KT and is 26mV at 27°C
- Mobility:
- The electron mobility and hole mobility have a similar doping dependence: For low doping concentrations, the mobility is almost constant and is primarily limited by phonon scattering. At higher doping concentrations, the mobility decreases due to ionized impurity scattering with the ionized doping atoms. The actual mobility also depends on the type of dopant.
- Mobility is linked to the total number of ionized impurities or the sum of the donor and acceptor densities.
- The minority carrier mobility also depends on the total impurity density. The minority-carrier mobility can be approximated by the majority-carrier mobility in a material with the same number of impurities.
- The mobility at a particular doping density is obtained from the following empiric expression:

- Resistivity:
- The resistivity is defined as the inverse of the conductivity. The conductivity of a material is defined as the current density divided by the applied electric field. Since the current density equals the product of the charge of the mobile carriers.
- To include the contribution of electrons as well as holes to the conductivity, we add the current density due to holes to that of the electrons.
- or:
![]()
- The conductivity due to electrons and holes is then obtained from:
![]()
- The resistivity is:

6. Poisson’s Equation
- Poisson’s equation correlates the electrostatic potential Φ to a given charge distribution ρ.
![]()
- Using the relation between the electric displacement vector and the electric field vector,
![]()
- where ε is the permittivity tensor. This relation is valid for materials with time independent permittivity. As materials used in semiconductor devices normally do not show significant anisotropy of the permittivity, can be considered as a scalar quantity ε in device simulation. The total permittivity is obtained from the relative εr and the vacuum permittivity ε0 as ε = εr ε0.
As ![]()
- can be expressed as a gradient field of a scalar potential field.

- Consider the permittivity a scalar, which is constant in homogeneous materials, we obtain Poisson’s equation.
![]()
- The space charge density ρ consists of :
ρ = q(p – n + C),
- where q is the elementary charge, p and n the hole and electron concentrations, respectively, and the concentration of additional, typically fixed, charges. These fixed charges can originate from charged impurities of donor (ND) and acceptor (NA) type and from trapped holes (ρp) and electrons (ρn),
C = ND – NA + ρp – ρn
- Poisson’s equation commonly used for semiconductor device simulation:
![]()
7. Continuity Equations
- The continuity equations can be derived using the following:
![]()
- By applying the divergence operator:
 , to the equation and considering that the divergence of the curl of any vector field equals zero.
, to the equation and considering that the divergence of the curl of any vector field equals zero.
![]()
- Separating the total current density
 into hole and electron current densities,
into hole and electron current densities, - and

- When we consider the charged impurities as time-invariant and introduce a quantity to split up the above equation into separate equations for electrons and holes, we get

- The quantity R gives the net recombination rate for electrons and holes.
- A positive value means recombination.
- A negative value means the generation of carriers.
If you aiming to crack GATE & ESE, Other PSU Exams then you must try Online Classroom Program to get unlimited access to all the live structured courses and unlimited mock tests from the following links:
ESE and GATE EC Online Classroom Program (24+ LIVE Courses and 150+ Mock Tests)
ESE and GATE EE Online Classroom Program (24+ LIVE Courses and 193+ Mock Tests)
Click on the Links Below to Avail Test Series:
Click Here Avail GATE/ESE EC Test Series !!! (150+ Mock Tests)
Click Here Avail GATE/ESE EE Test Series !!! (193+ Mock Tests)
Thanks


