Open Channel Flow
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The topic of open channel flow is one of the important topics for the GATE and other competitive exams. This topic consists of the flow in a channel open to the atmosphere, or the top surface of the fluid is under atmospheric pressure. Flow in a river, canal or partial flow in pipes comes under open channel flow.
Open Channel Flow PDF
Open channel flow can be of gradually varied flow or rapidly varied flow. Flow profiles in these flows will be different and governed according to the velocity of the fluid flow. This article contains basic notes on the “Open Channel Flow” topic of the “Fluid Mechanics & Hydraulics” subject.
Table of content
What is Open Channel Flow?
Open-channel flow, a branch of hydraulics and fluid mechanics, is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways but differ in one important aspect: the free surface.
- Open channel flow has a free surface, whereas pipe flow does not.
- Open channels can be natural or manmade conveyance structures has a free surface at atmospheric pressure. For example, flow in rivers, streams, and sanitary and storm
- sewers is partially full.
Types of Flow Possible in an Open Channel
Flow in an open channel can be classified based on velocity and other parameters. These types also depend on the variation of these flow parameters along the direction of flow along the length. Flow can be categorized as uniform, non-uniform, steady, and unsteady based on these parameters. The open channel flow is mentioned in the GATE CE syllabus. These are explained below.
Uniform Flow: If flow parameters like velocity, depth of flow, etc., are constant along the channel length, then the flow is said to be uniform. For such flows, ∂F/∂x = 0, where F is the flow parameter.
Non-uniform Flow: If flow parameters like velocity, depth of flow, etc., vary along the channel length, then the flow is considered to be a non-uniform flow. For such flows, ∂F/∂x ≠ 0, where F is the flow parameter.
Steady Flow: If flow parameters like velocity, depth of flow, etc., are constant with respect to time at a particular cross-section, then the flow is considered a steady flow. For such flows, ∂F/∂t = 0, where F is the flow parameter.
Unsteady Flow: If flow parameters like velocity, depth of flow, etc., vary with respect to time at a particular cross-section, then the flow is considered unsteady. For such flows, ∂F/∂t ≠ 0, where F is the flow parameter.
Specific Energy in Open Channel Flow
Specific energy is defined as the total energy at a particular cross-section of the open channel. It is equal to the datum head and the velocity head at the cross-section. In an open channel flow, the pressure head is considered because the flow in an open channel occurs under the atmospheric pressure head. With the help of specific energy of the flow, critical depth and critical discharge of flow can be estimated easily.
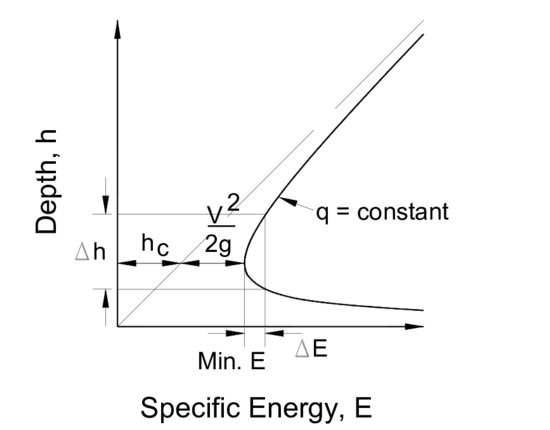
Critical Depth in Open Channel Flow
Critical depth corresponds to the critical flow occurring in the channel. Corresponding to the critical depth, specific energy in the flow will be minimum. Minimum energy at a particular section can only be possible for a single flow depth, called the critical depth. Critical depth depends on the type of section and the channel geometry. The value for the critical depth for rectangular and triangular channels can be expressed as follows.
- The specific energy of the flow is minimum and corresponds to the critical depth of flow.
- The flow parameters can be related to critical flow at a particular section as Q2T = gA3c. Where Q is discharge, T is top width, g is the acceleration due to gravity, and Ac is the cross-section area at critical flow.
- For rectangular flow, yc = (q2/g)(1/3) where q is the discharge per unit depth of the flow.
- For triangular flow, yc = (2Q2/gm)(1/5) where m is the slope of the side wall, and Q is the discharge flowing through the section.
Velocity Distribution in Open Channel Flow
Velocity distribution in an open channel depends on the type of channel and also the type of flow. For the non-uniform flow, the velocity distribution will be different; for the uniform flow, it follows another distribution. It will also depend on the geometry of the cross-section of the channel and is important for the GATE exam. Here velocity distribution for the different channels is shown below.
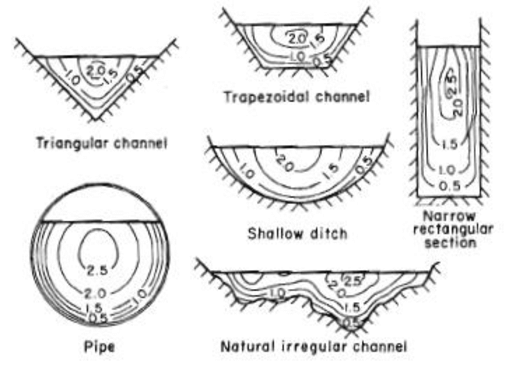
Different Flow Profiles in an Open Channel Flow
Different flow profiles in open channels depend on the type of flow. Types of flow can be different: gradually varied, rapidly varied, spatially varied, etc. Here few types of profiles for the gradually varied flow are explained below.
The type of profiles for gradually varied flow depends on the normal depth, critical depth and the actual depth of the flow. Here are a few types of profiles are shown below.
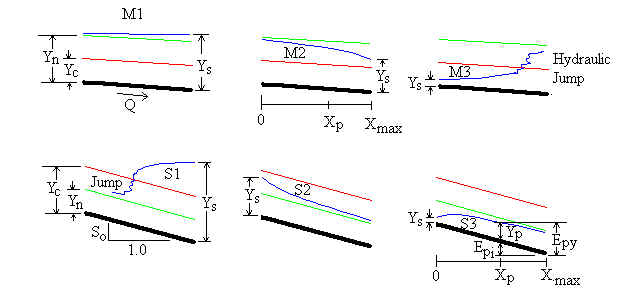
What is a Hydraulic Jump?
A hydraulic jump is a phenomenon of dissipating the energy of the flow. When the flow occurs at the supercritical depth, it requires dissipating some energy to reach the subcritical depth.
The hydraulic jump can be classified based on the Froude number of the flow, similar to flow through pipes. A Froude number is a dimensionless number defined as the ratio of inertia force to the gravitational force. Based on the Froude number of the flow, the hydraulic jumps can be classified into the following types:
- Undular Hydraulic Jump – 1 < Fr < 3
- Weak Jump – 3 < Fr < 6
- Oscillating Hydraulic Jump – 6 < Fr < 20
- Steady Hydraulic Jump – 20 < Fr < 80
- Strong Hydraulic Jump – Fr > 80
Here we are providing you with detailed sub-topic-wise handwritten notes, which will surely help you understand all the concepts related to Open Channel Flow.
| Handwritten Open Channel Notes | |
| Sub-Topic | Download Link |
| Uniform Open Channel Flow | Download PDF |
| Uniform Open Channel Flow Computations | |
| Bernoulli Principle in Open Channel Flow, Specific Head-Depth Diagram | |
| Application of Specific Head in Open Channel Flow, Super- and Sub-critical Flows | |
| Momentum Principle in Open Channel Flow | |
| Application of Momentum Principle in Open Channel Flow | |
| Gradually Varied Open Channel Flow | |
| Gradually Varied Flow Profiles | PDF, PDF |
| Examples of Gradually Varied Flow | |
| Unsteady Flow in Open Channels, Kinematic Waves | |
| Flood Routing | |



