Laminar Flow

Laminar Flow Over a Flat Plate

Flow over a flat plate can be classified into the laminar flow, turbulent flow or transition flow. This flow categorization is carried out based on the Reynolds number of the flow. Reynolds number of the flow depends on the flow velocity, fluid density and the characteristic dimension of the channel. Velocity in the laminar flow follows the parabolic distribution having zero velocity at the plate and equal to the stream velocity at the top layer. This velocity distribution of laminar flow is depicted below in the diagram.

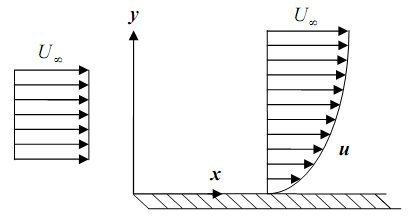
Laminar Flow Between Two Parallel Plates

The condition for the laminar flow between two parallel plates depends on the Reynolds number of the flow. In this case, the characteristics dimension is calculated in a different way than that for the flow over a flat plate.

Analysis of the Flow

Consider a fluid element in the flow field. An element has thickness dy, length dx and y distance from the bottom plate.

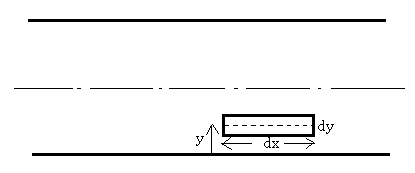
Assumption:- width of flow perpendicular to paper = unity

Free body diagram of an element

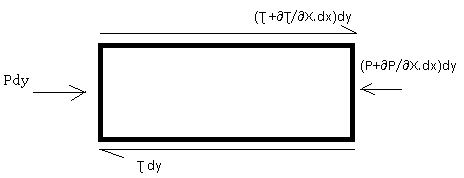
Apply equilibrium condition

But we know that

τ = μ du/dy

So,

μ d{(du/dy)}/dy = dp/dx …(1)

Where dp/dx and μ are independent form y

By integrating equation (1)

⇒ Again, integrate with respect to y

Apply boundary condition in this equation. Boundary condition includes the following points:

• No slip condition

At y = 0, u = 0
So, C₂ = 0

• Fluid velocity at the top and bottom plate is zero due to the action of frictional force.

At y=H, u=0

C₁ = (-H/2μ)(dp/dx)

So,

Maximum velocity

To find the maximum velocity of the fluid, the above velocity equation has been differentiated, and the maximum velocity can be found.

At y = H/2

u_max = (-H²/8μ)(dp/dx)

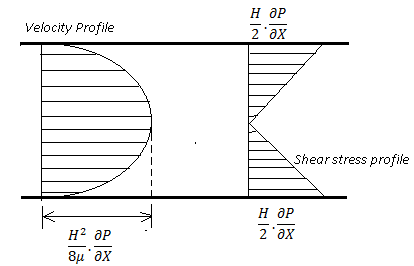
Shear Stress Distribution

By Newton’s Law of viscosity

The following diagram shows the velocity and shear stress distribution for the laminar flow below.

Pressure difference b/w two points along the flow

Consider average velocity expression

Laminar Flow Through Circular Pipe

In the circular pipe, flow can be either laminar, turbulent or transition. This can be categorized based on the Reynolds number of the flow. Flow velocities at the boundary of the circular pipe are zero and maximum at the centre of the pipe. Flow velocity for flow through a pipe, Shear stress distribution and other parameters are explained below.

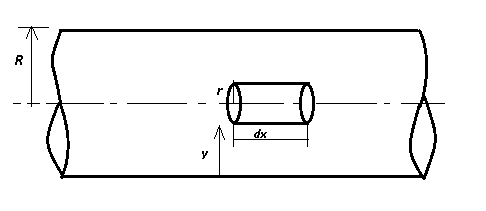
Consider a fluid element having radius r and length dx

Free body diagram of an element

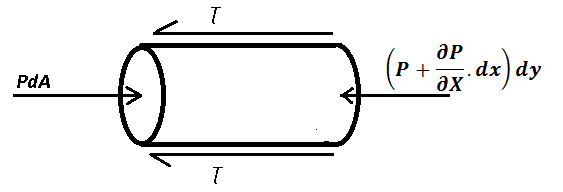
Apply horizontal equilibrium equation

Internal flow:-

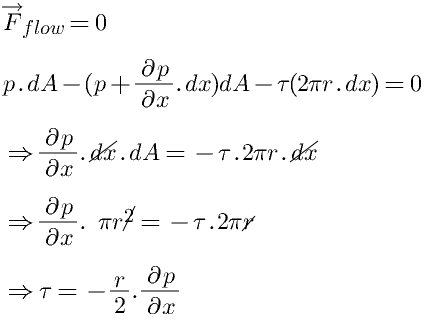
According to Newton’s Law of Viscosity

τ = μ (du/dy)

So, (-r/2)(dp/dx) = μ (du/dy) ….(a)

from the first figure in this section

y+r = R ⇒ dy = -dr

put the value of dy = -dr in eq. (a)

(-r/2)dp/dx = μ (du/dr)

⇒ du/dr = (r/2μ)(dp/dx)

By integrating it

u = r²/4μ(dp/dx) + C

At r=R, u=0 ⇒ no-slip condition

C = -R²/4μ(dp/dx)

So, u = 1/4μ(dp/dx)(R² – r²)

Maximum Velocity

V_max at r = 0

So from the expression of u, put r=0

u_r=0 = u_max = -R²/4μ(dp/dx)

Mean Velocity

The mass flow rate is constant throughout the pipe

From the expression of u_max and u_mean

⇒u_mean = u_max/2

Velocity and shear stress profile in a circular pipe

Velocity distribution and shear stress distribution along the pipe cross-section are depicted below.

Laminar Flow Reynolds Number

Flow can be categorized based on the Reynolds number of the flow. Reynolds number depends on the fluid velocity, viscosity and the characteristics dimension.

• ρ = density of the fluid
• V = Velocity of flow
• μ = Dynamic Viscosity
• D = Characteristic dimension

Head Loss Occured in Laminar Flow Through Pipes

head loss is one of the pipe’s important parameters of flow analysis. It is the loss of total energy head at a particular cross-section of pipes to any upstream section. The analysis of the head loss is carried out in the following way.

• Head loss for the laminar flow between Flat plate

Δp = 12μu_meanL/H²
H_L = Δp/ρg

H_L = 12μu_meanL/ρgH²

• Head loss for the laminar flow in a circular pipe

Δp = 32μu_meanL/D²
H_L = Δp/ρg

H_L = 32μu_meanL/ρgD²

 

If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE.

Online Classroom Program for ESE/GATE CE

You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams.

BYJU’S Exam Prep Test Series ESE/GATE CE

Important GATE Topics
Torsion Equation	Boolean Algebra Laws
Storage Class In C	Shear Flow
RSA Full Form	Difference Between Join And Union In SQL
Difference Between Clustered And Non-Clustered Index	Difference Between Commit And Rollback In SQL
Difference Between Multithreading And Multitasking	Types Of Stress