Laminar Flow
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Laminar flow is the type of flow characteristic, and it is classified based on the Reynolds number of the flow. Based on the Reynolds number of the flow, it can be characterized as the Laminar flow and the Turbulent flow. In laminar flow, Flow will occur in a layered form, and it can be studied by the study of flow patterns at a particular section.
Laminar Flow PDf
The velocity distribution follows the parabolic approach in the laminar flow. Mean and maximum velocity of the flow for laminar flow can be understood on the basis of the mass and momentum conservation of the fluid at a particular layer. This article contains basic notes on the “Laminar Flow” topic of the “Fluid Mechanics & Hydraulics” subject.
Table of content
What is Laminar Flow?
Laminar flow is a flow characteristic defined based on the Reynolds number of the flow. The Reynolds number of the flow is a dimensionless number, defined as the ratio of the Inertia force to the Viscous force. Laminar flow is also known as viscous flow because in laminar flow, viscous force is the predominant force, and it governs the flow behaviour.
In laminar flow, fluid particles move in a layered form in a streamlined way. So it is also called the streamlined flow. Laminar flow is essential for the GATE exam perspective. At the low velocity of the flow, fluid particles do not internally mix with each other; such fluid flows are named laminar flow. As the flow velocity increases, intermixing of the fluid particles starts, and such flow becomes a turbulent flow.
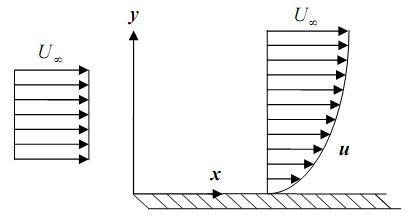
Laminar Flow Over a Flat Plate
Flow over a flat plate can be classified into the laminar flow, turbulent flow or transition flow. This flow categorization is carried out based on the Reynolds number of the flow. Reynolds number of the flow depends on the flow velocity, fluid density and the characteristic dimension of the channel. Velocity in the laminar flow follows the parabolic distribution having zero velocity at the plate and equal to the stream velocity at the top layer. This velocity distribution of laminar flow is depicted below in the diagram.
Laminar Flow Between Two Parallel Plates
The condition for the laminar flow between two parallel plates depends on the Reynolds number of the flow. In this case, the characteristics dimension is calculated in a different way than that for the flow over a flat plate.
Analysis of the Flow
Consider a fluid element in the flow field. An element has thickness dy, length dx and y distance from the bottom plate.
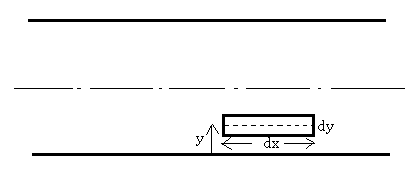
Assumption:- width of flow perpendicular to paper = unity
Free body diagram of an element
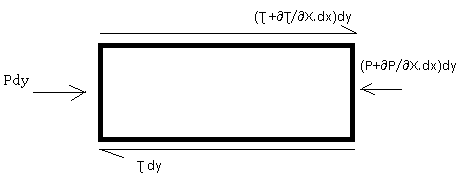
Apply equilibrium condition

But we know that
τ = μ du/dy
So,
μ d{(du/dy)}/dy = dp/dx …(1)
Where dp/dx and μ are independent form y
By integrating equation (1)

⇒ Again, integrate with respect to y

Apply boundary condition in this equation. Boundary condition includes the following points:
- No slip condition
At y = 0, u = 0
So, C2 = 0
- Fluid velocity at the top and bottom plate is zero due to the action of frictional force.
At y=H, u=0
C1 = (-H/2μ)(dp/dx)
So,

Maximum velocity
To find the maximum velocity of the fluid, the above velocity equation has been differentiated, and the maximum velocity can be found.
At y = H/2
umax = (-H2/8μ)(dp/dx)
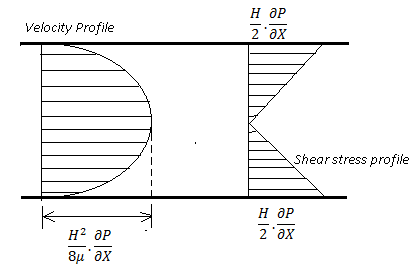
Shear Stress Distribution
By Newton’s Law of viscosity

The following diagram shows the velocity and shear stress distribution for the laminar flow below.
Pressure difference b/w two points along the flow
Consider average velocity expression

Laminar Flow Through Circular Pipe
In the circular pipe, flow can be either laminar, turbulent or transition. This can be categorized based on the Reynolds number of the flow. Flow velocities at the boundary of the circular pipe are zero and maximum at the centre of the pipe. Flow velocity for flow through a pipe, Shear stress distribution and other parameters are explained below.
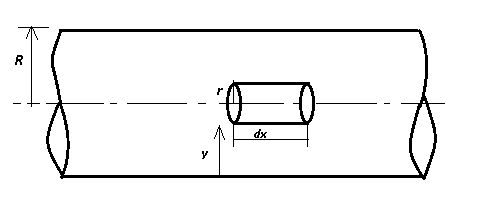
Consider a fluid element having radius r and length dx
Free body diagram of an element
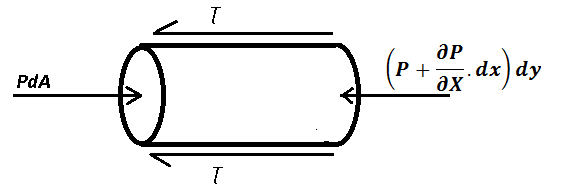
Apply horizontal equilibrium equation
Internal flow:-
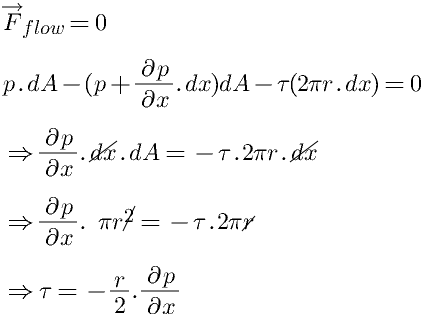
According to Newton’s Law of Viscosity
τ = μ (du/dy)
So, (-r/2)(dp/dx) = μ (du/dy) ….(a)
from the first figure in this section
y+r = R ⇒ dy = -dr
put the value of dy = -dr in eq. (a)
(-r/2)dp/dx = μ (du/dr)
⇒ du/dr = (r/2μ)(dp/dx)
By integrating it
u = r2/4μ(dp/dx) + C
At r=R, u=0 ⇒ no-slip condition
C = -R2/4μ(dp/dx)
So, u = 1/4μ(dp/dx)(R2 – r2)
Maximum Velocity
Vmax at r = 0
So from the expression of u, put r=0
ur=0 = umax = -R2/4μ(dp/dx)
Mean Velocity
The mass flow rate is constant throughout the pipe

From the expression of umax and umean
⇒umean = umax/2
Velocity and shear stress profile in a circular pipe
Velocity distribution and shear stress distribution along the pipe cross-section are depicted below.

Laminar Flow Reynolds Number
Flow can be categorized based on the Reynolds number of the flow. Reynolds number depends on the fluid velocity, viscosity and the characteristics dimension.
Here,
- ρ = density of the fluid
- V = Velocity of flow
- μ = Dynamic Viscosity
- D = Characteristic dimension
Re > 4000; For Turbulent Flow
- Head Loss equation by Darcy’s
HL = fLV2/2gD
Here f → Friction factor
V → Velocity (average)
L → Length of pipe
D → Diameter of pipe
This equation is valid for both turbulent and laminar flow. - Friction factor for circular pipe flow
In circular pipe
HL = 32μumeanL/ρgD2
But Darcey’s equation
HL = fLV2/2gD
By equating both expressions
fLV2/2gD = 32μumeanL/ρgD2
⇒ f = 64/(ρVD/μ) = 64/Re
Head Loss Occured in Laminar Flow Through Pipes
head loss is one of the pipe’s important parameters of flow analysis. It is the loss of total energy head at a particular cross-section of pipes to any upstream section. The analysis of the head loss is carried out in the following way.
- Head loss for the laminar flow between Flat plate
Δp = 12μumeanL/H2
HL = Δp/ρg
HL = 12μumeanL/ρgH2
- Head loss for the laminar flow in a circular pipe
Δp = 32μumeanL/D2
HL = Δp/ρg
HL = 32μumeanL/ρgD2
If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE.
Online Classroom Program for ESE/GATE CE
You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams.



