Flood Estimation [GATE Notes]
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The topic of flood estimation is one of the important topics of civil engineering from the perspective of the GATE and other competitive exams. Flood estimation is required to predict a flood in a particular catchment due to the existing precipitation. Several methods are available for flood analysis, including theoretical and analytical methods.
Flood Estimation PDF Notes
Flood estimation is required for the catchment basin to predict the condition of the flood. It is based on the previous year’s data on the rainfall that occurred in the catchment basin. This article contains fundamental notes on the “Flood Estimation” topic of the “Engineering Hydrology” subject.
Table of content
What is the Flood Estimation?
Flood estimation is one of the topics of engineering hydrology in which analysis of floods will be carried out. Flood estimation will be carried out based on the precipitation occurring in the catchment. Flood analysis is required to know the prevailing flood conditions for a particular catchment basin.
The estimation of flood analysis can be done based on various methods, including theoretical and analytical methods. These methods of flood analysis are important for the GATE CE exam and will be explained in this article.
Flood-Peak Estimation
A flood is an unusually high stage in a river, usually the level at which the river overflows its banks and inundates the adjoining area. The design of bridges, culvert waterways, and spillways for dams and the estimation of the score at a hydraulic structure are some examples wherein flood-peak values are required. To estimate the magnitude of a flood peak, the following alternative methods are available:
- Rational method
- Empirical method
- unit-hydrograph technique
- Flood-frequency studies
Rational Method
The most realistic way to use the Rational Method is to consider it as a statistical link between rainfall frequency distribution and runoff. As such, it provides a means of estimating the design flood of a certain return period, with the rainfall duration equal to the concentration time.
If tp ≥ tc
Qp = (1/36) k Pc A
Where,
- Qp = Peak discharge in m3/sec
- PC = Critical design rainfall in cm/hr
- A = Area catchment in hectares
- K = Coefficient of runoff.
- tD = Duration of rainfall
- tC = Time of concentration
Empirical Formulae
(a) Dickens Formula (1865)
Qp = CD A3/4
Where,
- Qp = Flood peak discharge in m3/sec
- A = Catchment area in km2.
- CD = Dickens constant, 6 ≤ CD ≤ 30.
(b) Ryes formula (1884)
Qp = CR A2/3
Where,
- CR = Ryes constant
- = 8.8 for the constant area within 80 km from the cost.
- = 8.5 if the distance of area is 80 km to 160 km from the cost.
- = 10.2 if the area is Hilley and away from the cost.
(c) Inglis Formula (1930)

Where
- A = Catchment area in Km2.
- QP = Peak discharge in m3/sec.
Flood Frequency Studies
Flood frequency analysis will be carried out to know the frequency of a particular flood that occurs at a certain interval. These analyses will be based on the different parameters, which will be explained below.
(i) Recurrence interval or return Period
T = 1/P
where, P = Probability of occurrence
(ii) Probability if non-occurrence: q = 1-P
(iii) Probability of an event occurring r times in ‘n’ successive years: = nCr x pr x qn-r
nCr = n! /(n-r)r!
(iv) Reliability: (probability of non-occurrence /Assurance) = qn
(v) Risk = 1-qn = 1-(1-P)n
(vi) Safety Factor = Design values of hydrological parameter adopted / Estimated value of the hydrological parameter
(vii) Safety Margin = Design value of the hydrological parameter – Estimated value of the hydrological parameter
Gumbel’s Method in Flood Estimation
The extreme value distribution was an introduction by Gumbel (1941) and is commonly known as Gumbel’s distribution. It is one of the most widely used probability distribution functions for extreme values in hydrologic and meteorologic studies for predicting flood peaks, maximum rainfall, and maximum wind speed.
Gumbel defined a flood as the largest of the 365 daily flows, and the annual series of flood flows constitute a series of the largest values of flows.
Based on the probability distribution.
![]()
(i) XT =X‾ + Kσ
Where
- XT = Peak value of hydrologic data
- K = Frequency factor

yT = Reduced variate

- T = Recurrence interval in year
- yn = Reduced mean = 0.577
- Sn = Reduced standard deviation.
- Sn = 1.2825 for N → ∞

Confidence Limit in Flood Estimation
Since the value of the variate for a given return period, xT is determined by Gumbel’s method. Which can have errors due to the limited sample data used. An estimate of the confidence limits of the estimates is desirable. The confidence interval indicates the limits to the calculated value between which the true value can lie with specific probability based on sampling errors only.
For a confidence probability c, the confidence interval of the variate xT is bounded by values x1 and x2 given by
X2/X1 = XT ± f(c).Se
Where f(c) is a confidence probability ‘C’ function. It can be represented as below.
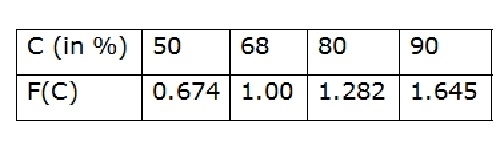
Se = Probability error
Where,
- N = Sample size
- B = factor
- σ = Standard deviation

![Flood Estimation [GATE Notes]](https://gs-post-images.grdp.co/2020/3/telegram_png30-1-img1585473029191-76.png-rs-high-webp.png)


