Crashing of Networks
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Crashing of networks is the phenomenon of reducing the overall duration of the project. The crashing of networks is carried out by deploying more resources to one or more activities. Deploying more resources is based on the cost slope of a particular activity in the project network.
By crashing of networks, the indirect cost of some activity gets reduced and the direct cost for the same activity will increase. The article contains fundamental notes on the “Crashing of Networks” topic of the “Construction Planning and Management” subject.
Table of content
What is the Crashing of Networks?
Crashing of activity refers to allocating more resources so that completion time for that activity and overall project time also reduce. You may change activity completion times by allocating more resources to it. Crashing of networks is mentioned in the GATE Electronics syllabus.
Crashing an activity (Crashing of networks): Reducing the time required to complete an activity (in hopes that this will reduce the completion time of the entire project) by assigning additional resources to that activity but reducing the duration time of the activities on the critical path may change the critical path.
- Normal time (NT): the expected time to complete an activity
- Normal cost (NC): the cost to complete the activity in its normal time
- Crash time (CT): the shortest possible time in which the activity can be completed
- Crash cost (CC): the cost to complete the activity in the shortest possible time (i.e., the cost to complete the activity in its crash time)
- Crash cost per time period = (CC – NC) / (NT – CT). It is also known as the cost slope of activity in the network.
Approaches to Crashing a Project Network
There are various approaches can be used for the crashing of networks. Crashing of networks simply means crashing a project network’s different activities. Here different methods are discussed which are used for the crashing of activities.
- Minimum-time schedule method:
- use the normal times for each activity to determine the critical path
- crash every activity from its normal time to its crash time (minimum duration time) – this gives the minimum-time schedule
If you must make the minimum time but want to reduce the cost, you can un-crash activities that aren’t critical, beginning with those that are most expensive.
- Minimum cost schedule method:
- use the normal times for each activity to determine the critical path
- crash the activity on the critical path that has the lowest cost to crash per unit of time until the activity duration time cannot be reduced any further, or another path becomes critical, or the additional costs of crashing outweigh savings from crashing
- repeat step 2 until the cost of continuing to crash the project is greater than the savings from crashing
- when there is more than one critical path, it may be necessary to simultaneously crash an activity on each path; if so, select the activities that give the lowest total cost per unit of time.
Generally, the distribution of the activity times is unknown and must be estimated. A typical method of dealing with the situation is to estimate three activity duration times for each activity, optimistic, most likely, and pessimistic. Use these estimates to estimate a normally distributed activity time:
Optimistic time (a): the probability of completing the activity in less than a is about 1%
Most likely time (m): the estimated average time required to complete the activity
Pessimistic time (b): the probability of taking longer than b is about 1%
The activity time is assumed to be normally distributed with mean, te, and variance as follows:
Expected time: te = ( a + 4m + b ) / 6
Variance: var[te] = [ ( b – a) / 6 ]2
Assumptions Involved in Crashing of Networks
Crashing of networks is done to reduce the overall duration of the project. it increases the direct cost and reduces the indirect cost of various resources. The crashing of networks is done with the help of many rules and assumptions. The assumptions are important for the GATE exam. These are described below.
1. Duration of activities along the critical path determines the project completion time
2. Duration time of one activity is independent of the duration times of all other activities. Using the Central Limit Theorem, the project completion time is assumed to be normally distributed with the mean equal to the sum of the activity times on the critical path and the variance equal to the sum of the variances of the activities on the critical path.
Once the mean and standard deviation of the critical path is known, it is possible to calculate the probability of completing the project in a certain time.
If a project has two critical paths, the critical path with the largest variance should be used to calculate the probability that the project will be completed within a certain time.
Note – Only considering the critical path makes a very strong assumption. In real situations, you should be aware of the other paths which may become critical. If an activity not on the critical path has a large variance of a duration time, it is possible for that activity to become a critical path activity simply through random occurrences.
Cost Model Analysis
In the CPM Cost Model, we will assume that project duration is reduced by deploying more resources to critical activities. To reduce the project’s overall duration, indirect cost decreases and direct cost increases. It should be in such a way that a reasonable cost is predicted for the optimum duration of the project.
Project Cost
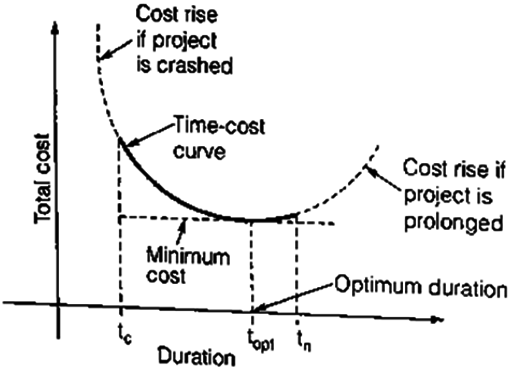
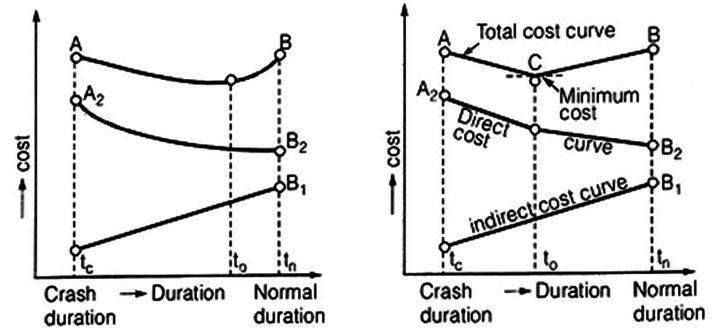
Total Project cost is the sum of two separate costs the direct cost of accomplishing the work, and the indirect cost related to the control or direction of that work, financial overhead, lost production, and the hike.
The components of the total cost are depicted in the figure
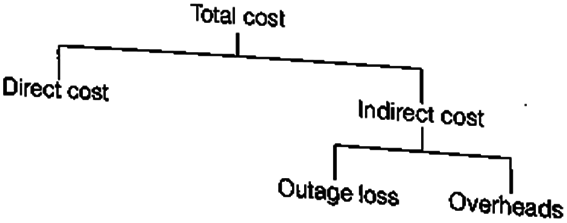
Components of Project Cost
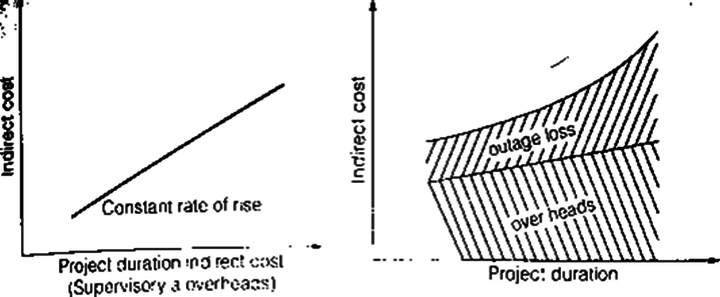
Indirect Project Cost: Indirect costs on a project are those expenditures that cannot be apportioned or allocated to the individual activities of a project but are assessed as a whole.
The indirect cost rises with increased duration.
The total indirect cost curve will thus be curved.
Direct Project Cost: These include labor cost, material cost, equipment cost, etc.
Normal time (tn): Normal time is the standard time that an estimator usually allows for an activity.
Crash time (tc): Crash time is the minimum possible time in which an activity can be completed by employing extra resources. Crash Time is that time beyond which any resource increase cannot shorten the activity.
Normal cost (Cn): This is the direct cost required to complete the activity in normal time duration.
Crash cost (Cc): This is the direct cost corresponding to the completion of the activity within crash time.
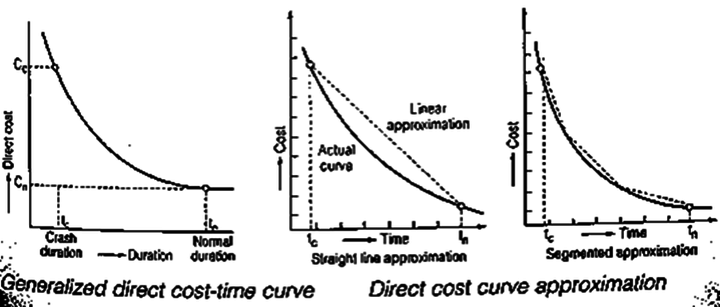
The straight line or segmented approximation of the direct cost curve helps carry out the project cost analysis. In such an analysis, the cost slope is used.
Cost Slope: The cost slope is the slope of the direct cost curve, approximated as a straight line. It is defined as follows:

Total Project Cost and Optimum Duration: The total project cost is the sum of the direct cost and indirect costs.
We find that the minimum total cost is obtained at some duration known as the optimum duration. The corresponding cost is known as the minimum cost. If the project duration is increased, the total cost will increase, while if the project duration is decreased to the crash value, the project cost will be the highest.
If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE.
Online Classroom Program for ESE/GATE CE
You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams.
BYJU’S Exam Prep Test Series ESE/GATE CE
Get complete information about the GATE exam pattern, cut-off, and all those related things on the Byju Exam Prep official youtube channel.



