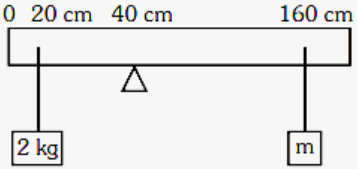
A uniform rod of length 200 cm and mass 500 g is balanced on a wedge placed at 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass ‘m’ is suspended from the rod at 160 cm mark as shown in the figure. Find the value of m such that the rod is in equilibrium (g = 10 ms⁻²).
By BYJU'S Exam Prep
Updated on: September 13th, 2023
- 1/2 kg
- ⅓ kg
- ⅙ kg
- 1/12 kg
We know that
The measure of the force which causes an object to rotate about an axis is the torque. The force causes an object to accelerate in linear kinematics. In a similar way, torque causes an angular acceleration. Therefore, torque is defined as the rotational equivalent of linear force.
The forces acting on the rod are shown in the figure below
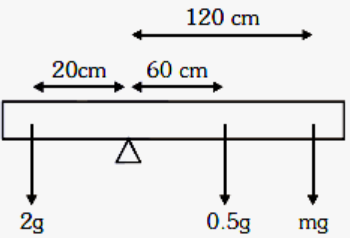
For the rod to remain in equilibrium
𝛕net = 0
Let us calculate the net torque of the wedge
2g x 20 = 0.5g x 60 + mg x 120
By further calculation
m = 0.5/ 6 kg = 1/12 kg
Therefore, the value of m is 1/12 kg.
Summary:
A uniform rod of length 200 cm and mass of 500 g is balanced on a wedge placed at the 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass ‘m’ is suspended from the rod at the 160 cm mark as shown in the figure. Find the value of m such that the rod is in equilibrium (g = 10 ms⁻2).
A uniform rod of length 200 cm and mass of 500 g is balanced on a wedge placed at the 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass ‘m’ is suspended from the rod at the 160 cm mark as shown in the figure. The value of m is 1/12 kg such that the rod is in equilibrium (g = 10 ms⁻2).
Related Questions:-
- A Circuit When Connected To An Ac Source Of 12 Volt Gives The Current Of 0 Point 2 Ampere Same Circuit When Connected To The Dc Source Of 12 Volt Gives A Current Of 0 Point 4 A?
- If The Magnitude Of The Resultant Of Two Vectors Of Equal Magnitudes Is Equal To The Magnitude Of Either Vectors?
- Explain The Process Of Digestion Of Food In Mouth Stomach And Small Intestine In Human Body?


