Resonance in RLC Circuit

What is Resonance in RLC Circuit?

We know that Resistor (R), Inductor (L), and Capacitor (C) are the passive elements. We can connect these passive elements in several ways. For the time being, let us consider the basic connections. These are series connections and parallel connections.

If we connect an AC source with variable frequency to the RLC network/ circuit combination, then at one frequency, the energy stored in both inductor and capacitor will be equal, or the net energy stored in the circuit will be zero. This frequency is known as resonant frequency, and we can say that the circuit is at resonance. In the RLC circuit the current at resonance is I = VR.

Types of Resonance in RLC Circuit

Since we have two basic connections, we will have two types of Resonance. Now, let’s discuss the following two types of resonances.

• Series Resonance
• Parallel Resonance

Resonance in Series RLC Circuit

In the series RLC circuit at resonance, we will connect the AC voltage source, Resistor (R), Inductor (L), and Capacitor (C), all in series. This circuit diagram is shown in the figure below.

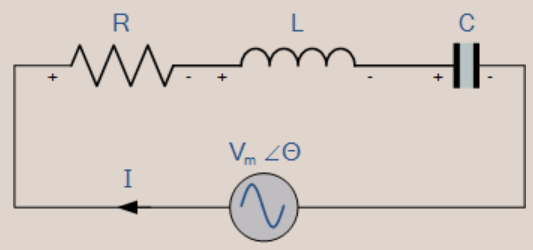
The current is the same in series, but the supply voltage (AC) gets divided among the passive elements.

• Since R, L, and C are connected in series, the equivalent impedance will be Z=R+j(ωL-1/ωC).
• The impedance, Z, will be real, equal to R when the imaginary part of impedance becomes zero at ω=0.
• At ω=ω₀, the inductor and capacitor reactance is the same.

ω₀L=1/ω₀C

=>ω₀2=1/LC

=>ω₀=1/√LC

=>f₀=1/2π√LC

• f0 is the series resonant frequency, equal to 1/2π√LC.
• At ω=ω₀, V=IZ=IR. That is, voltage and current are in phase at a resonant frequency. i.e., ∅=0.
• At the series resonant frequency, the power factor cos ∅ will equal 1. Hence, it is called a unity power factor.

Resonance in Parallel RLC Circuit

In a parallel RLC circuit, we will connect the AC source, Resistor (R), Inductor (L), and Capacitor (C) all in parallel. This circuit diagram is shown in the figure below.

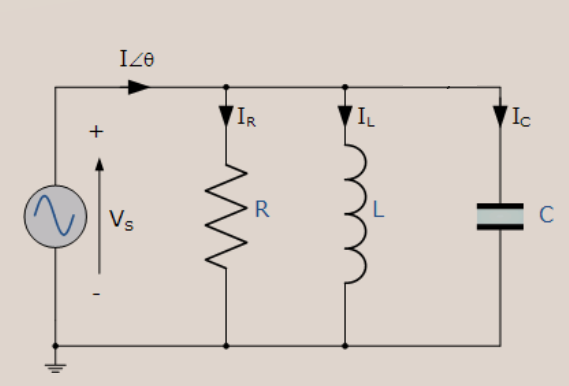
Voltage is the same, but the supply current (AC) gets divided among the passive elements.

• Since R, L and C are connected in parallel, and the equivalent admittance will be Y=1/R+j(ωC-1/ωL).
• The admittance, Y will be real, and it is equal to 1R when the imaginary part of admittance becomes zero at ω=ω₀.
• At ω=ω₀, the inductor and capacitor susceptance are the same.

ω₀C=1/ω₀L

=>ω₀2=1/LC

=>ω₀=1/√LC

=>f₀=1/2π√LC

• f₀ is the parallel resonant frequency, equal to 1/2π√LC.
• At ω=ω₀, I=VY=V/R. That is, current and voltage are in phase at a resonant frequency. i.e., ∅=0.
• The power factor at resonance in RLC parallel circuit is cos ∅ , which will equal 1. Hence, it is called a unity power factor.

Therefore, the power factor at resonance in the RLC circuit is equal to 1 for both series and parallel circuits. This article discussed resonance in RLC circuits for both series and parallel connections.