Shear Centre Formula, Definition and examples

What is Shear Centre?

The shear centre is defined as the point about which the external load must be applied to produce no twisting moment across the cross-section of the structural member. Loads must be applied at a particular point in the cross-section, called the shear centre if the beam is to bend without twisting. The shear centre is a point on which, if load acts; there will be no twisting of the cross-section, which means that only bending and direct stresses will act on the section. In general, it differs from the centroid of the body. The position of the shear centre will depend on the cross-sectional parameters.

The shear centre of the cross-section may differ from the centroid of the cross-section. And the distribution of the shear stress across the section depends on the geometry of the section and other cross-sectional parameters. The resultant of the shear stress for a particular cross-section acts on the point of the shear centre of the section. For a doubly symmetric cross-section, the shear centre and centroid of the section will coincide. The transverse load will result in a bending moment and twisting moment for a beam if it is not applied at the shear centre, but if it is applied on the shear centre, then it will only cause a bending moment to the cross-section.

Shear flow in the cross-section of the body governs by the position of the shear centre. Shear flow is the variation of shear stress along the section of the body, which helps to find the shear force acting on a particular section. Hence overall shear flow is an important parameter of designing the structural member.

Download Civil Engineering Short Notes for Fluid Mechanics 

Definition Of Shear Centre

An enteral centre is where a shear force can act without producing any twist in the sectionnter. In such conditions, only bending stresses will act over the section.

Download Formulas for GATE Civil Engineering – Solid Mechanics

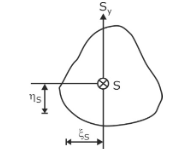
Location of Shear Centre

The shear centre for a member is the point at which, if the load is applied, it will cause no twisting to the centre. The location of the shear centre can be found by equating the moment due to external force to the total resisting moment for a particular section. Here a general expression for a section is explained below with the help of the following diagram.

Unsymmetric Loading of Thin-Walled Members

The Beam loaded in a vertical plane of symmetry deforms in the symmetry plane without twisting.

A beam without a vertical plane of symmetry bends and twists under loading.

If the shear load is applied such that the beam does not twist, then the shear stress distribution satisfies the following equation.

F and F’ indicate a couple of Fh and the need for applying torque and the shear load. It can be expressed as Fh = Ve

Shear Stress Distribution Strategy

• Determine the location of centroid and I_yy, I_zz and I_yz as needed – (symmetric sections subject to V_y needs only I_zz)
• Divide the section into elements according to geometry (change in slope)
• Start with a vector following the element centre line from a free end
• Calculate the first moment of the area. This determines the shear flow distribution
• A negative shear value indicates the direction of shear flow opposite to the assumed vector
• Calculate the first moment of the area. This determines the shear flow distribution

Shear stress distribution for symmetric sections subject to bending about one axis

• For elements parallel to the bending axis- Linear distribution

• For elements normal to bending axis- Parabolic distribution

For unsymmetric sections, shear flow in all elements is parabolic

When moving from one element to another, the end value of shear in one element equals the initial value for the subsequent element (from equilibrium)

Shear Centre Formula

The Thcenterr centre formula can be determined with the help of its properties. Some steps need to be followed to find this location, described below.

• It will always lie on the axis of symmetry.
• If there is more than one axis of symmetry, it lies at the intersection of symmetrical axes.
• If there is one axis of symmetry and one axis of asymmetry, then it lies on the axis of symmetry in such cases.
• If the section is made up of two narrow rectangles, then it will be located on the axis of symmetry of both rectangles.

Shear Centre of Channel Section 

The shear centre lies on the centre of the axis of symmetry. If there is symmetry between axes, the shear centre lies at the intersection of the axes. But the Channel section is a section that is symmetrical about its x-axis and unsymmetrical about its y-axis. The Shear centre of the channel section lies on the x-axis of the channel section.

Shear Centre Of Semicircular Arc

The shear centre for an arc lies outside the arc, and at this point, if total load acts, it will cause no twisting to the section, and the section remains in the bending and axial stress condition. The centre’s location depends on the geometry of the crostini; it will not depend upon material properties. In the below-mentioned diagrcenterar centre, the semicircular arc is depicted, which will help to understand the position of the centre.

Shear Centres for Some Other Sections

As we discussed, if the load is applied on the shear centre, it will cause no twisting to the cross-section. So, it is important to know the shear centre for the section used in constructing the structures. Here a few commonly used structural sections and their shear centre are given for proper understanding.

• Symmetric cross-sections

Doubly symmetric cross sections- Coincides with centroid

Singly symmetric cross sections- Lies on the axis of symmetry

• Unsymmetric cross-sections

For thin-walled open sections- The opposite side of the open part

What Is Shear Flow

Shear flow is a term used in solid mechanics and fluid dynamics. The general expression for shear flow represents shear stress along the distance of a cross-section in a thin-walled shell or any structure. Shear flow is also defined as what is induced by an external force.

Variation of the shear flow at a given cross-section can also be expressed by equation VQ/I. This equation is simply the value of the multiplication of shear stress and the thickness of the member.

What are the Pressure Vessels?

Pressure vessels are storage tanks specially designed to resist the effect of external pressure. Types of pressure vessels can be classified mainly into two types, which are explained below.

• Thin shells

If the thickness of the wall of the shell is less than 1/10 to 1/15 of its diameter, then the shell is called a thin shell.

t < (D_i / 10) to (D_i / 15)

• Thick shells

If the thickness of the wall of the shell is greater than 1/10 to 1/15 of its diameter, it is called a thick shell.

t > (D_i / 10) to (D_i / 15)

Where the nature of stress in a thin cylindrical shell subjected to internal pressure

1. Hoop stress/circumferential stress will be tensile in nature.
2. Longitudinal stress/axial stress will be tensile in nature
3. Radial stress will be compressive in nature.

Stresses in Thin Cylindrical Shell

• Circumferential Stress /Hoop Stress

σ_h = pd/2t ≥ pd/2tη

Where p = Intensity of internal pressure

d = Diameter of the shell

t = Thickness of shell

η = Efficiency of joint

• Longitudinal Stress

σ_l = pd/2t ≥ pd/2tη

• Hoop Strain

ε_h = pd (2 – μ)/4tE

• Longitudinal Strain

ε_L = pd (1 – 2μ)/4tE

• The ratio of Hoop Strain to Longitudinal Strain

ε_h/ε_L = (2 – μ)/(1 – 2μ)

• Volumetric Strain of Cylinder

ε_v = pd (5 – 4μ)/4tE

Stresses in Thin Spherical Shell

• Hoop stress/longitudinal stress

σ_L = σ_h = pd/4t

• Hoop stress/longitudinal strain

ε_L = ε_h = pd (1 – μ)/4tE

• Volumetric strain of sphere

ε_L = 3pd (1 – μ)/4tE

Assumptions of Lame’s Theory for analysis of Thick Cylinders

1. Homogeneous, isotropic and linearly elastic material.
2. The plane section of the cylinder, perpendicular to the longitudinal axis, remains the plane.

If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE:

Online Classroom Program for ESE/GATE CE

You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams:

BYJU’S Exam Prep Test Series ESE/GATE CE

Other Important GATE Notes
Steel	Zero Force Member In A Truss
Errors in measurements	Creep of Concrete
Lami’s Theorem	Random and systematic error
Macaulay’s Method	Tender in Construction
Critical Path Method	Rate Analysis