Determine the current in each branch of the network shown in figure 3.30:
By BYJU'S Exam Prep
Updated on: September 13th, 2023
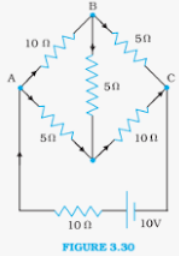
The current flowing through the various branches of the circuit is shown in the figure
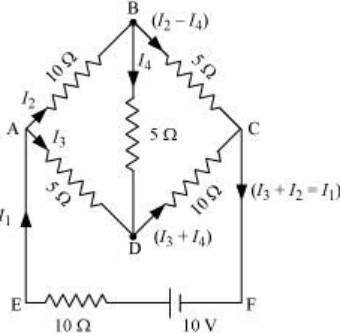
I1 is the current flowing through the outer circuit
I2 is the current flowing through the branch AB
I3 is the current flowing through the branch AD
I2 – I4 is the current flowing through the branch BC
I3 + I4 is the current flowing through the branch CD
I4 is the current flowing through the branch BD
The potential is zero for the closed circuit ABDA
10I2 + 5I4 – 5I3 = 0
Dividing the equation by 5
2I2 + I4 – I3 = 0
I3 = 2I2 + I4 …. (1)
The potential is zero for the closed circuit BCDB
5 (I2 – I4) – 10 (I3 + I4) – 5I4 = 0
5I2 – 5I4 – 10I3 – 10I4 – 5I4 = 0
5I2 – 10I3 – 20I4 = 0
I2 = 2I3 + 4I4 …. (2)
The potential is zero for the closed circuit ABCFEA
-10 + 10 I1 + 10 I2 + 5 (I2 – I4) = 0
10 = 15I2 + 10I1 – 5I4
3I2 + 2I1 – I4 = 2 …. (3)
Using the equation (1) and (2)
I3 = 2 (2I3 + 4I4) + I4
I3 = 4I3 + 8I4 + I4
-3I3 = 9I4
-3I4 = I3 …. (4)
Substituting equation (4) in (1)
I3 = 2I2 + I4
-4I4 = 2I2
I2 = -2I4 …. (5)
From the figure, it is evident that
I1 = I3 + I2 …. (6)
Substituting equation (6) in (1)
3I2 + 2 (I3 + I4) – I4 = 2
5I2 + 2I3 – I4 = 2 …. (7)
Substituting equations (4) and (5) in (7)
5 (-2I4) + 2 (-3I4) – I4 = 2
-10I4 -6I4 – I4 = 2
17I4 = -2
I4 = -2/17 A
So the equation (4) reduces to
I3 = -3I4 = -3 (-2/17) = 6/17 A
I2 = -2I4 = -2 (-2/17) = 4/17 A
I2 – I4 = 4/17 – (-2/17) = 6/17 A
I3 + I4 = 6/17 + (-2/17) = 4/17 A
I1 = I3 + I2 = 6/17 + 4/17 = 10/17 A
In branch BC = 6/17 A, CD = 14/17 A, AD = 6/17 A and BD = -2/17 A
So the total current at C = (I2 – I4) + (I3 + I4) = 6/17 + 4/17 = 10/17
Therefore, the current in each branch is BC = 6/17 A, CD = 14/17 A, AD = 6/17 A and BD = -2/17 A.
Summary:
Determine the current in each branch of the network shown in figure 3.30
The current in each branch of the network is BC = 6/17 A, CD = 14/17 A, AD = 6/17 A and BD = -2/17 A.
Related Questions:-
- 50 Kg Of Nitrogen And 10 Kg Of Hydrogen Are Mixed To Produce Ammonia Calculate The Ammonia Formed And Identify The Limiting Reagent In The Production Of Ammonia In This Situation?
- Distinguish Between Biodegradable And Non Biodegradable Substances List Two Effects Of Each Of Them On Our Environment?
- Two Metallic Oxides Contain 27 Point 6 Percent And 30 Percent Oxygen Respectively If The Formula Of The First Oxide Is X3o4 The Formula Of The Second Will Be?


