- Home/
- CDS & Defence/
- Article
The compressibility factor for an ideal gas is: (A) 1.5 (B) 1.0 (C) 2.0 (D) Infinity
By BYJU'S Exam Prep
Updated on: September 25th, 2023
The compressibility factor for an ideal gas is 1.0. Since the molecules in this hypothetical gas clash totally elastically (there is no loss of energy), the gas law is applicable. Some characteristics of Ideal gas are mentioned below:
- They are minute molecules with minimal volume, resembling tiny points.
- No attracting or repelling force affects the interactions between gas particles.
- When the gases collide with the container’s walls, they ought to be completely elastic (no energy loss).
Table of content
Compressibility Factor of Ideal Gas
The ideal gas law equation is provided by
PV = nRT
Where
V = volume of the gas,
R = 8.314 J/mol-K (Universal Gas constant),
P = pressure of the gas
T = gas temperature.
n = moles of gas,
Real Gas: They can be both repulsive and alluring, depending on the molecules. It will only follow the gas law at high temperatures and low pressure. The molecules’ bulk is not negligible. Following is the Van der Waals equation:
(P + an2/V2) × (V – n b) = n R
- They found that at high pressures and low temperatures, all gases depart from their ideal behavior. More differences are present in the majority of soluble and liquefiable gases.
- All recognized gases are actual gases. Amagat, Andrew, and other scientists studied the behavior of several gases under various pressure and temperature conditions.
- So, compared to gases like carbon dioxide, sulfur dioxide, and ammonia, gases like hydrogen, oxygen, and nitrogen show a far lesser divergence.
- We plot the compressibility factor vs pressure P to show how the gases deviate from the ideal behavior given by Z = PV/nRT.
The characteristics of the graph are:
- At moderate pressure, Z 1, with a negative deviation, nRT > PV, the gases in this region are more compressible.
- All curves get nearer to their ideal states as the pressure falls and approaches zero. As a result, at absolute zero pressure, the gases behave as ideal gases. The Z value of ideal gases is 1. In the case of ideal gases, PV = nRT.
- Positive deviation and decreased compressibility of the gases compared to ideal gases are caused by high pressure, Z > 1.
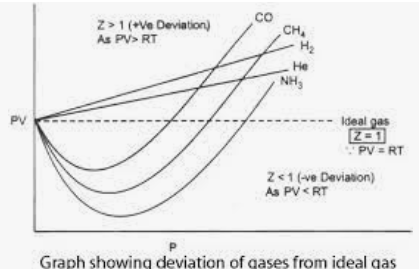
As a result, an ideal gas has a compressibility factor of one.
Summary:
The compressibility factor for an ideal gas is: (A) 1.5 (B) 1.0 (C) 2.0 (D) Infinity
An Ideal gas has a compressibility factor of 1. To identify the Ideal gas, you need to understand its characteristics first. Some examples of IDeal gases are nitrogen, oxygen, hydrogen, noble gases, and some heavier gases like carbon dioxide.
