Conditional Probability Study notes for GATE CSE
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Conditional Probability Study notes for GATE CSE- Conditional probability is defined as the possibility of an event, based on the circumstances of a past event. Conditional probability is derived by multiplying it by the previous event. Read below in detail about the basics of probability, conditional probability and Bayes theorem for important competitive exams like GATE CSE, etc.
Table of content
BASICS PROBABILITY
We perform an experiment that can have a number of different outcomes. The sample space is the set of all possible outcomes of the experiment. We usually call it S.
For example, if I plant ten bean seeds and count the number that germinates, the sample space is
S = {0,1,2,3,4,5,6,7,8,9,10}.
If I toss a coin three times and record the result, the sample space is
S = {HHH,HHT,HTH,HTT,THH,THT,TTH,TTT},
where (for example) HTH means ‘heads on the first toss, then tails, then heads again.
An event is a subset of S. We can specify an event by listing all the outcomes that make it up. In the above example, let A be the event ‘more heads than tails’ and B the event ‘heads on the last throw’. Then
A = {HHH,HHT,HTH,THH}
B = {HHH,HTH,THH,TTH}
Probability = Favorable number of cases/Total Number of cases
Hence if asked what is the probability of event A in the above example, then
Probability = n(A)/n(S) = 4/8 = 0.5
We can build new events from old ones:
• A∪B (read ‘A union B’) consists of all the outcomes in A or in B (or both!)
• A∩B (read ‘An intersection B’) consists of all the outcomes in both A and B;
• A\B (read ‘A-minus B’) consists of all the outcomes in A but not in B;
• A’ (read ‘A complement’) consists of all outcomes, not in A (that is, S \A);
• Ø (read ‘empty set’) for the event which doesn’t contain any outcomes

Independent Events:
Two events A and B are said to be independent if
P(A∩B) = P(A)·P(B)
Mutually Exclusive Events:
Two events A and B are said to be mutually exclusive if
P(A∩B) = 0
Collectively Exhaustive Events:
Two events A and B are said to be collectively exhaustive if
P(AUB) = 1

CONDITIONAL PROBABILITY
Let E be an event with non-zero probability, and let A be any event. The conditional probability of A given E is defined as
P(A | E) = P(A∩E) /P(E)
Example: A random car is chosen among all those passing through Trafalgar Square on a certain day. The probability that the car is yellow is 3/100: the probability that the driver is blonde is 1/5, and the probability that the car is yellow and the driver is blonde is 1/50. Find the conditional probability that the driver is blonde given that the car is yellow.
Solution: If Y is the event ‘the car is yellow’ and B the event ‘the driver is blonde’, then we are given that P(Y) = 0.03, P(B) = 0.2, and P(Y ∩B) = 0.02. So
P(B | Y) = P(B∩Y) / P(Y) = 0.02 /0.03 = 0.667
BAYES’ Theorem
There is a very big difference between P(A | B) and P(B | A).
Let A and B be events with non-zero probability. Then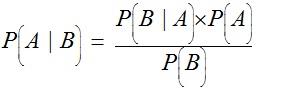


So this was about the basics of probability and conditional probability. Practice questions now from the practice section in the app.
You can follow the detailed champion study plan for GATE CS 2021 from the following link:
Detailed GATE CSE 2021 Champion Study Plan
Candidates can also practice 110+ Mock tests for exams like GATE, NIELIT with BYJU’S Exam Prep Test Series check the following link:
Click Here to Avail GATE CSE Test Series! (100+ Mock Tests)
Get unlimited access to 21+ structured Live Courses all 112+ mock tests with Online Classroom Program for GATE CS & PSU Exams:
Click here to avail Online Classroom Program for Computer Science Engineering
|
Related Links |
|
| GATE CSE Exam Analysis 2022 | |
| BARC CS Syllabus | |
| BARC CS Exam Analysis | |
Thanks
Prep Smart. Score Better!
Download BYJU’S Exam Prep, Best gate exam app for Preparation


