Introduction to Propositional & Predicate Logic (Part-1) Study Notes
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Introduction to Propositional & Predicate Logic Study Notes- Proposition: A declarative sentence whose value is either true, or false, but not both, is known as a proposition.
Table of content
Examples of the proposition:
(1) Delhi is the capital of India.
(2) 1 + 2 = 4, this is also a propositional whose truth value is false.
Examples of not proposition:
(1) “Read this carefully” is not because it is not a declarative sentence.
(2) x + 1 = 2, This is also not, here x is variable, where x can take any value make the statement true or false.
Compound Proposition
It is a proposition formed using the logical operators (Negation(~), Conjunction(^), Disjunction(v) etc.) with the existing propositions.
Logical Operators
(i) Negation of p: ~p
(ii) Conjunction of p and q: p ^ q
(iii) Disjunction of p and q: p v q
(iv) Implication/Conditional:
Other ways to express
“If p, then q” “p implies q”
“if p, q” “p only if q”
“p is sufficient for q” “q whenever p”
“q if p” “q unless ~p”
“q when p” “a sufficient condition for q is p”
“a necessary condition for p is q”
(v) Bi-conditional:
Other ways to express
“p is necessary and sufficient for q”
“if p then q, and conversely”
“p iff q”
The precedence order of logical operators from high to low:
- Converse: The proposition q p is called the converse of p q.
- Inverse: The proposition ~p ~q is called the inverse of p q.
- Contrapositive: The contrapositive of p q is the proposition ~q ~p.
Note: Among all these three only the contrapositive always has the same truth value as p q.
What is Tautology?
An assertion or compound proposition that is true always, regardless of what the truth values of the individual propositions occurred in it, is referred to as a tautology.
Example: p v ~p
What is Contradiction?
If the Compound proposition is always false then it is Contradiction.
Example: p ^ ~p
What is Contingency?
A compound proposition that is neither a tautology nor a contradiction is called a contingency.
Example: p
What is Logical Equivalence?
p q is a tautology if p and q are logically equivalent.
What is Functionally Complete?
If any formula can be written as an equivalent formula containing only the connective in a set of operators, then such a set of operators is called functionally complete.
Example: {~, ^}, {~, V}, {~, ^, V} are functionally complete.
Equivalences
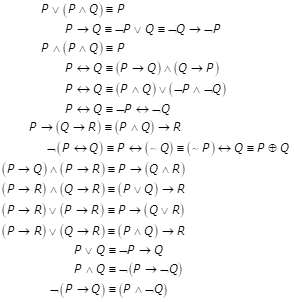
Logical Equivalences laws
Identity Laws:
(i) P ^ T = P (ii) P v F = P
Domination Laws:
(i) P v T = T (ii) P ^ F = F
Idempotent Laws:
(i) P ^ P = P (ii) P v P = P
Commutative Laws:
(i) P v Q = Q v P (ii) P ^ Q = Q ^ P
Associative Laws:
(i) (P v Q) v R = P v (Q v R)
(ii) (P ^ Q) ^ R = P ^ (Q ^ R)
Distributive Laws:
(i) P v (Q ^ R) = (P v Q) ^ (P v R)
(ii) P ^ (Q v R) = (P ^ Q) v (P ^ R)
De Morgan’s Laws:
(i) ~(P ^ Q) = ~p v ~Q
(ii) ~(P v Q) = ~p ^ ~Q
Absorption Laws:
(i) P v (P ^ Q) = P
(ii) P ^ (P v Q) = P
Negation Laws:
(i) P v ~P = T (ii) P ^ ~P = F
Double Negation Laws:
~(~P) = P
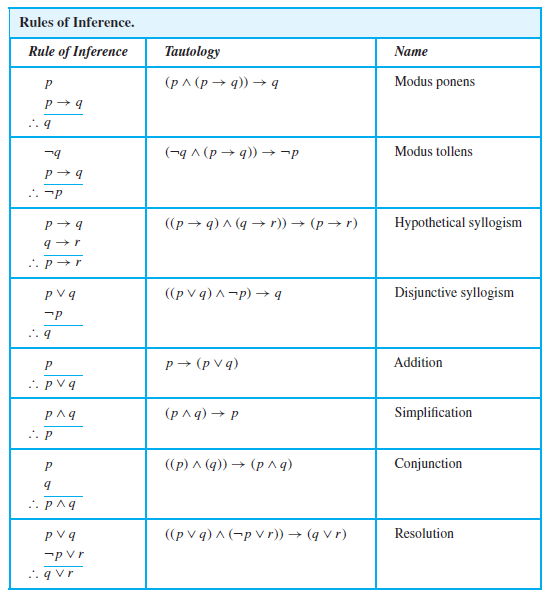
RULES OF INFERENCE (TAUTOLOGICAL IMPLICATIONS)
You can follow the detailed champion study plan for GATE CS 2022 from the following link:
Detailed GATE CSE 2022 Champion Study Plan
Candidates can also practice 110+ Mock tests for exams like GATE, NIELIT with BYJU’S Exam Prep Test Series check the following link:
Click Here to Avail GATE CSE Test Series! (100+ Mock Tests)
Get unlimited access to 21+ structured Live Courses all 112+ mock tests with Online Classroom Program for GATE CS & PSU Exams:
Click here to avail Online Classroom Program for Computer Science Engineering
|
Related Links |
|
| GATE CSE Exam Analysis 2022 | |
| BARC CS Syllabus | |
| BARC CS Exam Analysis | |
Thanks
Sahi Prep Hai Toh Life Set Hai
Download BYJU’S Exam Prep, Best gate exam app for Preparation


