Limits & Continuity Study Notes for GATE CSE
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Limits & Continuity Study Notes for GATE CSE- A limit is an idea of looking at what happens to a function as you approach particular values of x. Left-hand and right-hand limits are the thought of watching what happens to a function as you approach a specific value of x, from a specific direction.
Table of content
Limits
The limit of f(x) as x approaches the worth of a from the left is written.
and the limit of f(x) as x approaches the value of a from the right is written
Definition of a Limit at a Point
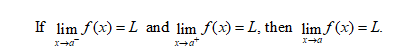
Therefore, if the left-hand limit does not equal the right-hand limit as x approaches a, then the limit as x approaches a does not exist.
Limits found Numerically and Algebraically
While most limits are often found graphically, as we’ve been discussing, it’s not always practical or necessary if the function is defined algebraically.
For instance, say we are given that. If we are looking for, we can find both the left- and right-hand limits by using tables. By choosing x values that meet up with and closer to x = 3 from each side, we will analyze the behaviour of f(x)
|
|
Limit from the left |
|
limit from right | ||||
|
x |
2.99 |
2.999 |
2.9999 |
3 |
3.0001 |
3.001 |
3.01 |
|
f(x) |
5.99 |
5.999 |
5.9999 |
6.00 |
6.0001 |
6.001 |
6.01 |
Notice that when we chose values on either side of x = 3, they were values that were very on the brink of x = 3. It seems that as x approaches 3 from either side, the function values are approaching 6. Therefore, it seems reasonable to conclude that.
Making tables can still be as time-consuming as graphing, so we’ll use the subsequent rules to algebraically evaluate limits more efficiently. Most of those rules can intuitively be verified from watching the previously worked examples.
Continuity
A function f(x) is continuous at x = a, if all of the following are true:
Continuity means that a function is continuous wherever the graph of the function has no holes, gaps, or jumps. A function is claimed to be discontinuous at x = a, if a hole, gap, or break occurs within the graph at x = a, meaning the function violates one of the three items above.
Notice that the third item is within the definition of continuity and Rule.
Example.
Using the graph of f(x) below, find all values of x where f(x) is discontinuous and state why f(x) is discontinuous at these points, according to the definition of continuity.
Solution:
x = -3, f(-3) is undefined
x = -2, f(-2) is undefined
x = 1, while the function is defined by f(1)=5 and ,
these are unequal and thus the third item of the definition is violated
x = 4, and does not exist.
An important formula of limit

Differentiability
Suppose y = f (x), then its derivative with respect to x, is commonly denoted by
f ′(x) = y′ = D f (x) = Dx f (x)
The symbols and D are called differential operators. They are used to explicitly denote the differentiation of the function that follows
Basic Differentiation Formulas:
Suppose f and g are differentiable functions, c is any real number, then
You can go with the detailed champion study plan for GATE CS 2021 from the following link:
Detailed GATE CSE 2021 Champion Study Plan
Candidates can also practice 110+ Mock tests for exams like GATE, ISRO, DRDO, BARC, NIELIT, etc. with the BYJU’S Exam Prep Test Series check the following link:
Click Here to Avail GATE CSE Test Series! (100+ Mock Tests)
Get unlimited access to 21+ structured Live Courses, all 112+ mock tests with the Online Classroom Program for GATE CS & PSU Exams:
Click here to avail Online Classroom Program for Computer Science Engineering
|
Related Links |
|
| GATE CSE Exam Analysis 2022 | |
| BARC CS Syllabus | |
| BARC CS Exam Analysis | |
Thanks
Prep Smart. Score Better!


