- Home/
- CDS & Defence/
- Article
State and prove converse of BPT (basic proportionality theorem).
By BYJU'S Exam Prep
Updated on: September 25th, 2023
The converse of the Basic proportionality theorem (BPT): According to this theorem, if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. The Basic Proportionality Theorem, often known as the Thales Theorem, was developed by the eminent Greek mathematician Thales. He asserted that the ratio of any two matching sides is constant for any two equiangular triangles. He developed the basic proportionality theorem based on this idea (BPT).
Table of content
Prove Converse of BPT
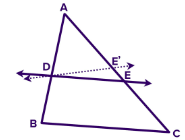
Let’s say that a line DE intersects AB and AC’s two sides at D and E, as shown;
AD/DB = AE/EC ….. (i)
Assume DE and BC are not parallel. Next, connect BC and DE’ with a straight line.
thus, using similar triangles:
AD/DB = AE’/E’C …. (ii)
From eq. (i) and (ii), we get;
AE/EC = AE’/E’C
Adding 1 on both sides:
AE/EC + 1 = AE’/E’C + 1
(AE + EC)/ EC = (AE’ + E’C)/ E’C
AC/EC = AC/E’C
EC = E’C
This is only feasible if E and E’ coincide.
But DE’ || BC
Therefore, DE || BC
Hence, proved
Summary:
State and prove converse of BPT (basic proportionality theorem).
Contrary to the Basic Proportionality Theorem (BPT), a line is parallel to the third side if it divides any two sides of a triangle in the same ratio. It’s been proven.
