- Home/
- CDS & Defence/
- Article
A farmer moves along the boundary of a square field of side 10m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
By BYJU'S Exam Prep
Updated on: September 25th, 2023
A farmer moves along the boundary of a square field of side 10m in the 40s. The magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position will be 10√2m.
Step 1: collecting the given data
A farmer walks the perimeter of a square field with a side of 10 meters in 40 seconds.
Step 2: Now we can use the formula
Speed = distance/time
Step 3: Calculating the farmer’s speed
Finding the farmer’s displacement from his starting position after 2 minutes and 20 seconds is important. We have that, the side of square ABCS is x = 10 m
The perimeter of the square = 4 x side = 4x = 4 x 10 = 40 m
It is assumed that the farmer circles this square field once in 40 seconds. Because of this, the farmer covered 40m in 40 seconds.
Speed of farmer = distance/ time = 40m/40s = 1m/s
Step 4: determining the farmer’s travel distance
Now we have to figure out how far the farmer traveled in 140 seconds, or 2 minutes and 20 seconds. The same speed formula yields
Speed = distance/time
1 = distance/140
Distance = 140 m
Thus, the farmer covered 140 meters in 2 minutes and 20 seconds.
Step 5: Estimating the magnitude of the displacement
The position of the farmer on the border of square ABCD must now be calculated after two minutes and twenty seconds. The perimeter of the square = one round of the square
40m = 1 round
1m = 1/40 round
140m = 1/40 x 140 = 3.5 rounds
As a result, the farmer takes 2 minutes and 20 seconds to complete 3.5 circuits of the square field ABCD. The net displacement from the starting location is zero when the farmer completes one clockwise rotation of square field ABCD beginning at vertex A. As a result, after three rounds, there has been no net displacement.
After 0.5 rounds, the farmer arrives at the location diagonally opposite to its beginning position, i.e. point C if it starts at vertex A of square field ABCD. The diagonal AC of the square field is equal to the net displacement from the beginning location. As a result, after 3.5 rotations, the farmer’s net displacement equals the diagonal AC of the square field.
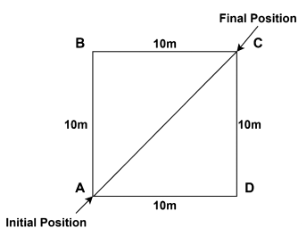
Right-angle triangle ADC is the result of using Pythagoras’ Theorem.
Hypotenuse2 = Base2 + Height2
AC2 = AD2 + AB2
AC2 = 102 + 102
AC2 = 200
AC = √200
AC = 10√2m
Consequently, the farmer’s net displacement after 3.5 rounds is equal to 102m. The farmer’s displacement from his starting position after two minutes and twenty seconds is therefore 10√2m.
Summary:
A farmer moves along the boundary of a square field of side 10m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
A farmer walks 40 seconds along the perimeter of a square field with a side of 10 meters. The farmer will have moved 10 m away from his starting point after 2 minutes and 20 seconds. It can be calculated using the Pythagoras theorem
