UGC NET Study Notes On Square of Opposition (Logical Reasoning)

 1. Proposition: A proposition is a sentence that makes a statement and gives a relation between two or more terms. In logical reasoning, any statement is termed as a proposition.

• A proposition is assumed to be true and from which a conclusion can be drawn.
• The statement, ‘all dogs are lemons’ is assumed to be true as a proposition (or premise), but actually we all know that dogs and lemons are entirely different entities.

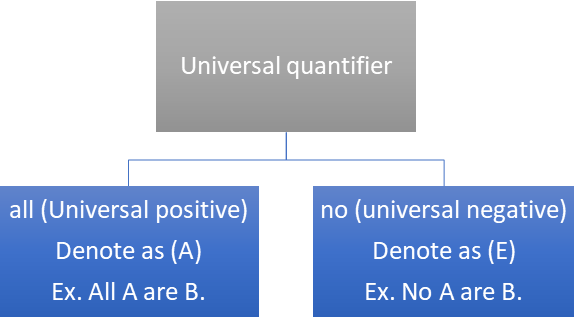
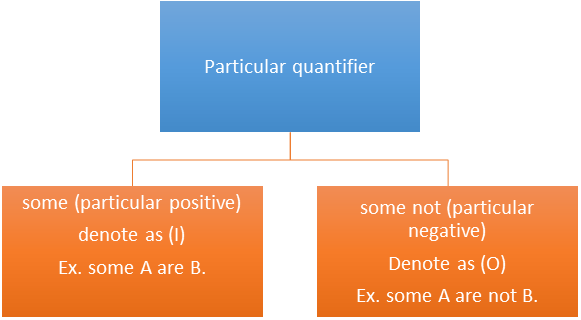
The proposition consists of the following four parts:

1. Quantifier: all, no and some. They specify a quantity. ‘all’ and ‘no’ are universal quantifiers and ‘some’ is a particular quantifier.
2. Subject: About which something is being said.
3. Predicate: Something that affirms or denies the subject.
4. Copula: The relation between subject and predicate.

2. Classical Square of Opposition: The categorical proposition having the same subject and predicate terms may differ in quality and quantity or in both. This differs is called opposition.

• There were few questions in previous years exam, where understanding terms, such as contradictory, contrary, sub alternation and sub contrary may help in finding solutions.
• The understanding of the square of opposition can help candidates in attempting these types of questions:

a. Contradictory: Contradictory opposition is the relation between two proposition having the same subject but differs in both quality and quantity. The relation between A and O, E and I are called contradictory. In order to refute the truth of the proposition ‘All dogs are lemons’, it would be enough to show that some dog (or even one dog) are not lemon. One exception would disprove the truth of the universal affirmative proposition.

b. Contrary: Contrary opposition exists between two proposition when both have universal quantity but one affirms and the other denies its predicate of the subject. The relationship between A and E is called contraries.

Ex: (A) All dogs are lemons: This statement is universal affirmative.

The contrary of this proposition will be: (E) No dogs are lemons. This statement is universal negative.

c. Sub contraries: The relation between two particular proposition having the same subject and predicate but differing in quality is sub contrary opposition. The relation between particular affirmative (I) and particular negative (O) is called sub contraries.

Ex. Some dogs are lemons (I): This is a particular positive proposition.

Sub contrary to the proposition will be: Some dogs are not lemons (O): This is a particular negative proposition.

d. Sub alternation: Sub alternation opposition is the relation between two proposition having the same subject and predicate but differing in quantity only.

The relation between universal negative (E) and particular negative (O) is called sub alternation.

Check this table to see all the differences between Square of Opposition Terms

Questions from previous year papers

1. "E" denotes:

(A) Universal Negative Proposition

(B) Particular Affirmative Proposition

(C) Universal Affirmative Proposition

(D) Particular Negative Proposition

Ans: A

‘E’ denotes universal negative proposition.

Ex. No cats are apple.

2. If the statement ‘all students are intelligent’ is true, which of the following statements are false?

(i) No students are intelligent.

(ii) Some students are intelligent.

(iii) Some students are not intelligent.

(A) (i) and (ii)

(B) (i) and (iii)

(C) (ii) and (iii)

(D) (i) only

Ans: B

Solution: This statement  ‘all students are intelligent’ is a universal positive proposition. If universal positive is true, then definitely particular negative will be false because of the contradictory relationship. And contradictory of this statement is ‘some students are not intelligent’. In a contrary relationship, if universal positive is true then universal negative must be false. And universal negative of this statement is ‘no students are intelligent’.

We hope you are going through these concepts daily to make you prepare for UGC NET 2023.

Try Online Classroom Program Now and get unlimited access to 12+ structured live courses and 200+ Mock tests.

Thank You.

Score Better.

Team BYJU'S Exam Prep.