What do you mean by Free Vibration?
Free vibration refers to the natural motion of a mechanical system that occurs when it is disturbed from its equilibrium position and then left to vibrate with no external force acting on it. The system will oscillate at its natural frequency, which is determined by its mass and stiffness properties. In free vibration, the motion amplitude will eventually decrease due to energy loss through friction, damping, or other types of energy dissipation. This phenomenon of the system returning to the equilibrium position on its own is called free vibration.
The system can be a single-degree-of-freedom system like a spring-mass system or a multi-degree freedom system like complex structures. In single-degree-of-freedom systems, the motion can be described by a simple harmonic motion (SHM) equation, and the natural frequency is given by √(k/m), where k is the spring constant and m is the mass of the system. In multi-degree-of-freedom systems, the natural frequencies can be found by solving the eigenvalue problem of the system. It's also important to note that free vibration does not mean the system has no energy dissipation; it's just the absence of external force. The system can still have internal energy dissipation, such as friction and damping, which will ultimately cause the amplitude of the vibration to decay over time.
Free Vibration Formula
The mathematical derivation of free vibrations involves solving a set of differential equations that describe the system's motion. The equations are based on the system's mass, stiffness, and damping properties.
The equation of motion for a single degree of freedom system under free vibration can be written as:
mx'' + cx' + kx = 0
Where:
m = mass of the system c = damping coefficient k = spring constant x = displacement of the system
This is a second-order homogeneous differential equation with constant coefficients, which can be solved using various methods. One common method is to use the method of natural frequencies, which involves assuming a solution of form x(t) = eλt
We can then plug the solution into the differential equation and solve for λ, obtaining the eigenvalue problem as λ² + cλ/m + k/m =0
Solving this equation for λ gives the solution for the system's natural frequency. The solution for the displacement x is the combination of two or more natural frequencies or the mode shape of the system. For multi-degree-of-freedom systems, the equation of motion can be represented as a matrix form of the equation, and the natural frequencies and mode shapes can be found by solving the eigenvalue problem. Solving the equation of motion can be complex and require knowledge of mathematical methods such as the Laplace Transform, Fourier series, etc. But overall, it is the key step to understanding and predicting the behaviour of mechanical systems under free vibrations.
Types of Free Vibration
There are two main types of free vibrations: Transient vibration, which occurs when a system is first disturbed from its equilibrium position, and steady-state vibration, which occurs once the system has reached a constant amplitude and frequency. Additionally, free vibrations can be classified as undamped, damped, or forced depending on whether there is energy dissipation, such as friction or damping, or an external force is applied to the system. There are two main types of free vibrations:
Transient vibration: It is the vibration which occurs in the system when it is disturbed from its equilibrium position. The system oscillates for a short period of time until it reaches its steady-state vibration. The initial vibration is usually very high, and it decreases with time. The system returns to its steady state vibration due to internal energy dissipation.
Steady-state vibration: It is the system's vibration after it has reached its steady state. The amplitude of the vibration becomes constant and occurs at a fixed frequency, known as the system's natural frequency. The natural frequency of a system is determined by the mass and stiffness properties.
It is also worth mentioning that there are other classifications of free vibrations, such as:
- Undamped Free Vibrations: Free vibrations of the system without energy dissipation such as friction or damping
- Damped Free Vibrations: Free vibrations of the system with energy dissipation such as friction or damping.
- Forced Free Vibrations: Free vibrations of the system which are excited by an external force
Generally, the type of free vibration that occurs in a system depends on the specific system, its properties and the disturbance that causes it.
Application of Free Vibration
Free vibration has many engineering applications, including designing and analysing mechanical systems, identifying natural frequencies and mode shapes, vibration isolation, structural health monitoring, noise and vibration control, dynamic balancing and maintenance schedule. Free vibration is a fundamental concept in mechanical vibrations and is used in many engineering applications to improve mechanical systems' safety, reliability, and efficiency. Free vibration has many engineering applications, including:
Design and analysis of mechanical systems: Understanding a system's natural frequencies and mode shapes under free vibration is important for designing safe and efficient mechanical systems. It also helps engineers to predict the system's response to external loads.
Identification of natural frequencies and mode shapes: By analyzing a system's behaviour under free vibration, it's possible to identify its natural frequencies and mode shapes. This information can be used to design and optimize the system's performance.
Vibration isolation: By understanding the natural frequencies of a system, it's possible to design isolation systems to reduce unwanted vibrations. This can be achieved by designing a system with a natural frequency different from the frequency of the unwanted vibration.
Structural Health Monitoring: By analyzing the free vibration characteristics of a structure, it is possible to monitor the structural integrity and detect any damage, such as cracks, corrosion, or looseness of bolts.
Noise and Vibration Control: Free vibrations can control unwanted noise and vibration. Introducing a controlled amount of vibration at the right frequency can cancel out or reduce the amplitude of unwanted vibrations.
Dynamic balancing: Free vibration can be used to balance the rotor of the machine dynamically by adjusting the position of the mass of the rotor
Maintenance schedule: By monitoring changes in the amplitude or frequency of the system's free vibration over time, it is possible to schedule maintenance and detect wear or damage early, which helps to prevent unplanned downtime and costly repairs.
Free vibration is a fundamental concept in mechanical vibrations and is used in many engineering applications to improve mechanical systems' safety, reliability, and efficiency.
Advantages of Free Vibration
Free vibration has several advantages, including improved design and analysis of mechanical systems, vibration isolation, structural health monitoring, noise and vibration control, dynamic balancing and maintenance schedule. It also identifies natural frequencies and mode shapes and predicts the system's response to external loads. Free vibration has several advantages in certain engineering and industrial applications. These include:
Improved design and analysis: Understanding a system's natural frequencies and mode shapes under free vibration make it possible to design and optimize its performance.
Vibration isolation: By analyzing the natural frequencies of a system, it's possible to design isolation systems to reduce unwanted vibrations.
Structural Health Monitoring: Free vibration can be used to monitor the structural integrity and detect any damage, such as cracks, corrosion, or looseness of bolts.
Noise and Vibration Control: Free vibrations can control unwanted noise and vibration. Introducing a controlled amount of vibration at the right frequency can cancel out or reduce the amplitude of unwanted vibrations.
Dynamic balancing: Free vibration can be used to balance the rotor of the machine dynamically by adjusting the position of the mass of the rotor
Maintenance schedule: By monitoring changes in the amplitude or frequency of the system's free vibration over time, it is possible to schedule maintenance and detect wear or damage early, which helps to prevent unplanned downtime and costly repairs.
Overall, Free vibration is an important concept in the study of mechanical vibrations, and its advantages are in the design and analysis of systems, the identification of natural frequencies and mode shapes, the prediction of the system's response to external loads, vibration isolation, structural health monitoring, noise and vibration control, dynamic balancing and maintenance schedule.
Limitations of Free Vibration
The limitations of free vibration include limited control, complex systems, lack of internal energy dissipation considerations, limited applicability to real-world loading conditions, not suitable for systems under external forces and limited predictability. Free vibration only provides insight into how the system will behave under certain conditions and may not always provide accurate predictions or practical solutions. Some limitations exist to using free vibration in certain engineering and industrial applications. Some of the main limitations include the following:
Limited control: Free vibrations are determined by a system's natural frequencies and mode shapes, which may be difficult to control or change.
Complex systems: Analyzing free vibrations in systems such as multi-degree-of-freedom systems or systems with distributed mass and stiffness can be challenging and require advanced mathematical and computational methods.
Energy dissipation: Free vibrations may not account for internal energy dissipation, such as friction and damping, which can affect the system's performance and response to external loads.
Real-world loading conditions: Free vibrations may not accurately simulate real-world loading conditions, as natural vibrations are often more complex and variable.
Limited in the analysis of systems with external forces: Free vibration only considers the internal properties of the system; it is not suitable for systems under external forces or excitation.
Limited predictability: Free vibration only provides insight into how the system will behave under certain conditions. It does not predict the system's behaviour under different loads or environments.
Overall, free vibration is a useful tool for understanding the behaviour of mechanical systems under certain conditions, but it has its limitations and may not always provide accurate predictions or practical solutions. It's important to consider these limitations when using free vibration in engineering and industrial applications.
Natural Vibrations
Natural vibrations, also known as normal modes or eigenmodes, are the vibrational patterns of a mechanical system when it is in its equilibrium state and subjected to no external forces. Natural vibrations are an essential part of the GATE ME syllabus. These vibrations occur at the system's natural frequencies, which are determined by the mass and stiffness of the system. A system may have multiple natural frequencies, each corresponding to a different vibrational pattern.
A system's natural frequencies and vibrational patterns are important to understand because they can affect its stability and response to external forces. In some cases, the natural vibrations of a system may be used to intentionally excite certain frequencies to perform a specific function, such as in the operation of a tuning fork or a musical instrument.

Fig.2: Spring-mass System
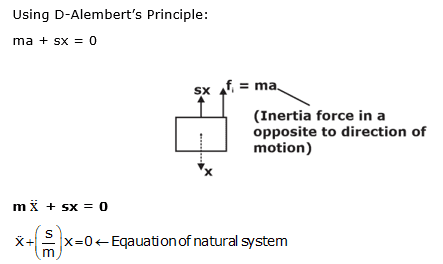
Energy Method to Calculate the Natural Frequency
This method is used only for natural vibrations and especially for Rolling problems. Various NAT-based questions in the GATE exam are formulated using this method.
In Natural Vibrations,
As kinetic friction = 0
Total energy = constant

Get complete information about the GATE exam pattern, cut-off, and all those related things on the BYJU’S Exam Prep official youtube channel.






Comments
write a comment