Boolean Logic: Expression, Theorems, Operations, Examples
By BYJU'S Exam Prep
Updated on: September 25th, 2023

For the binary system, Boolean logic was developed as a type of algebra. English mathematician George Boole proposed this algebra in the year 1854. The numbers 0 and 1, or True and False, are used in this application of Aristotle’s propositional logic. Binary variables and logic operations are the focus of Boolean algebra.
In this article, we will cover all the basics of Boolean Logic, Boolean algebra, and how Boolean expressions are used to evaluate a result into zero and one truth values.
Table of content
What is Boolean Logic?
Boolean logic is widely used in digital electronics as a form of algebra. The idea of Boolean Logic is that all the expressions or values are true or false. It mainly uses three basic Boolean operators: OR operator, AND operator, and NOT operator.
Because it works well with the binary numbering system, in which each bit can either have a value of 1 or 0, Boolean logic is particularly crucial for computer science. A different perspective would be that each bit has a value of either TRUE or FALSE.
Boolean Expression for Logic Gates
A logical statement that can only be TRUE or FALSE is called a Boolean expression. Any form of data can be compared using Boolean expressions as long as both portions of the expression use the same fundamental data type. Data can be tested to see if it is more than, equal to, or less than other data.
A Boolean expression can consist of Boolean information or data, such as the following:
- Boolean formulas consist of Boolean variables.
- Boolean Values in the form of TRUE or False or in the binary form 1 or 0, respectively.
- Functions result in Boolean values(0 or 1) or Boolean expressions.
Boolean Theorems
Theorems in Boolean algebra are employed to alter the form of Boolean expressions. Boolean theorems may be applied to an expression to reduce its number of minterms. Digital logic has the following Boolean algebraic theorems and laws:
- DeMorgan’s Theorem: (A.B)’ = A’ + B’
- Consensus Theorem: AB + A’C + BC= AB+ A’C
- Duality Theorem
- Redundant Theorem
- Complementary Theorem
Boolean Logic Operations
Conjunction, disjunction, and negation are the three fundamental Boolean logic operations. The related binary operators AND, OR, and the unary operator NOT, collectively referred to as Boolean operators, are used to express these Boolean operations.
The truth table for the basic boolean algebra operations is as follows:
OR Operation
|
A |
B |
A OR B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
AND Operation
|
A |
B |
A AND B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
NOT Operation
|
A |
NOT A |
|
0 |
1 |
|
1 |
0 |
Boolean Logic Example
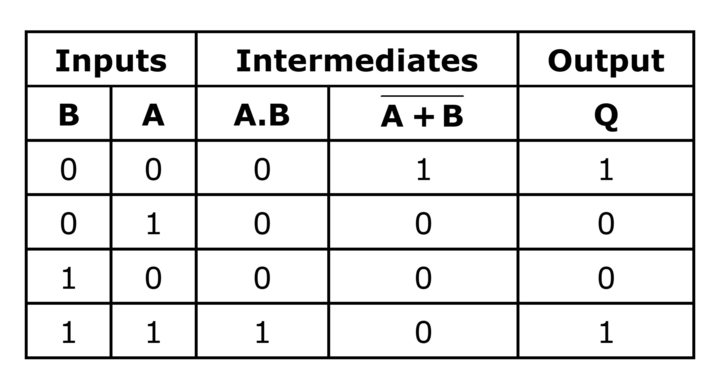
Find the Boolean algebra expression for the given logic system.
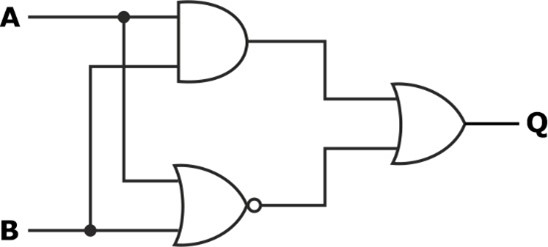
Solution:

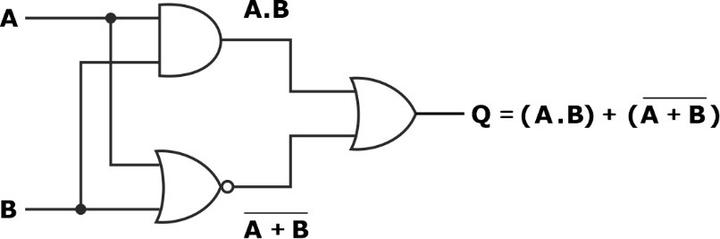

The truth table for the above circuit is: