What is NAND Gate?

What is a NAND Gate?

The NAND gate is a AND gate followed by a NOT gate. Thus, we can say it is a AND NOT operation. It may have two or more inputs but only one output.

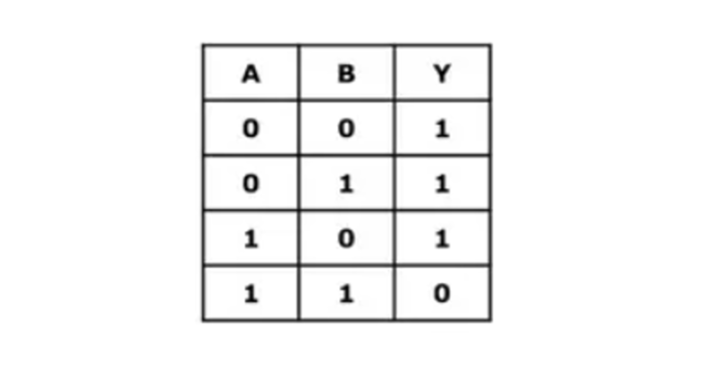
NAND Gate Truth Table

The truth table of NAND Gate is shown below:

NAND Gate Symbol

The logical symbols of the NAND gate are shown below:

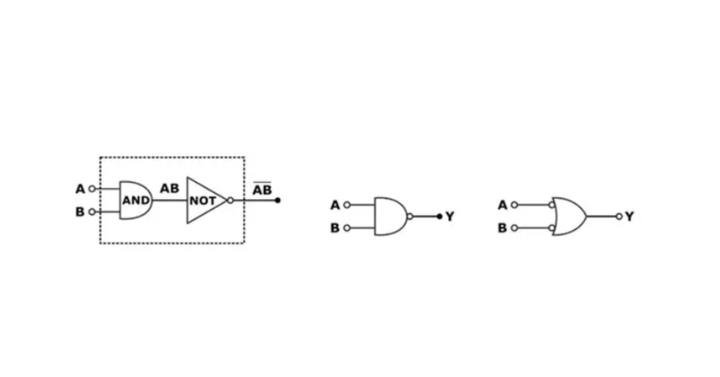
NAND Gate Logical Expression

Thus, the logical expression for the output is:

__    ___      __  __
Y  =  A.B  =  A +B

Download Formulas for GATE Computer Science Engineering – Computer Organization & Architecture

NAND Gate Switching Diagram

It is clear from the NAND gate truth table of the two-input NAND gate that the output is 1 when either A or B or when both the inputs are at logic ‘0’. We can say that if Ā = 1 = B, both A and B are 1, and the output is 1. Therefore, the NAND gate can perform the OR function by inverting the inputs.

• The output is the exact inverse of the AND gate for all possible input combinations in the NAND gate.
• The OR gate with inverted inputs is called bubbled OR gate or negative OR gate. The NAND gate is also called an active low OR gate.
• The switching circuit diagram for a NAND gate is shown below.

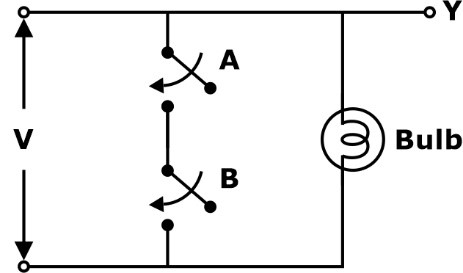
The bulb will glow when any of the switches A or B will open (logic 0).

• NAND gate follows the commutative law as (AB)’ = (BA).’

• NAND gate will not follow the associative law as

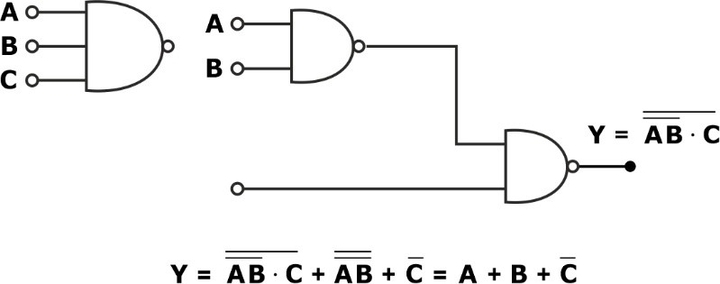
• Enable and disable inputs:
  For a NAND Gate

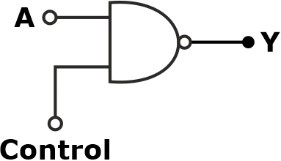
For control = 0;

A	Control	Y
0	0	1
1	0	1

Thus, logic ‘0’ is the disabled input for the NAND gate.

For control = 1;

A	Control	Y
0	1	1
1	1	0

Thus, logic ‘1’ is the enabled input for the NAND gate.

Download Formulas for GATE Computer Science Engineering – Operating Systems

Uses of NAND Gate

The NAND gate’s popularity is because it is the simplest of the digital logical operators to implement using transistor technology. This simple circuit was used to build the early microprocessors.

NAND gates detect a single low input in a digital system. A simple security system made up entirely of NAND gates. For example, the NAND gate monitors monitor the status of sensors connected to windows or doors. The sensor sends the security system a logical 1 signal when a window or door is closed. The alarm output is when all windows and doors are closed. When a single window or door is opened, the security system output changes to 1, which can be used to trigger an alarm or perform another action.

Advantages of NAND gate

NAND gates are low-cost devices with large storage capacities for their size. The NAND gate has good replaceability, which means that if the flash memory becomes damaged, it can be replaced with an appropriate component.
NAND gate memory capacity can replace large files such as USB drives, digital cameras, and tablets. The NAND gate has extreme endurance and durability.

Realization of the Logic Gate Using NAND Gate

In Boolean Algebra, the NAND gate is called a universal gate because any digital circuit can be implemented by using any one of these two i.e. any logic gate can be created using NAND gate.

NOT Gate Realization

For the NOT gate realization, we require 1 NAND gate as shown in the circuit diagram:

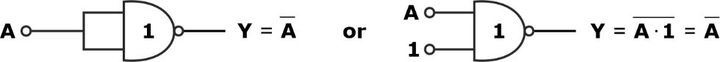
AND Gate Realization

For the AND gate realization, we require 2 NAND gates, as shown in the circuit diagram:

OR Gate Realization

For the OR gate realization, we require 3 NAND gates if the inputs are not available in complement form, as shown in the circuit diagram:

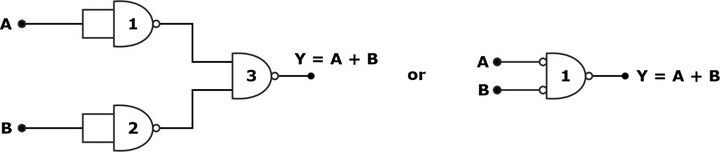
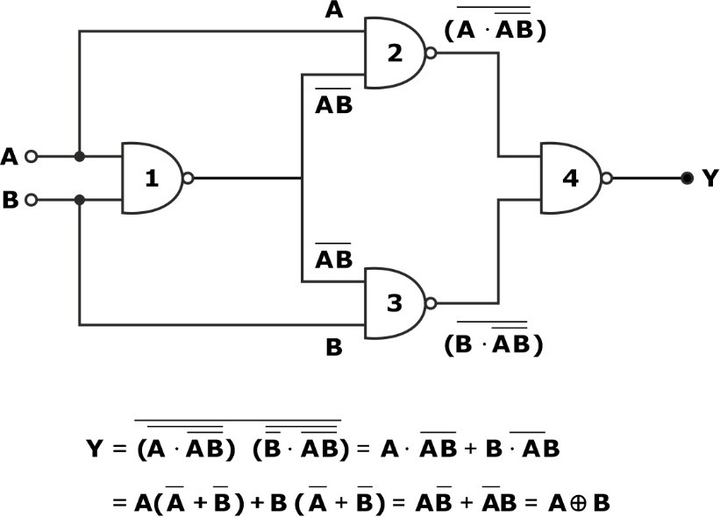
EX-OR Gate Realization

For the EX-OR gate realization, we require 4 NAND gates, as shown in the circuit diagram:

EX-NOR Gate Realization

For the EX-NOR gate realization, we require 5 NAND gates, as shown in the circuit diagram:

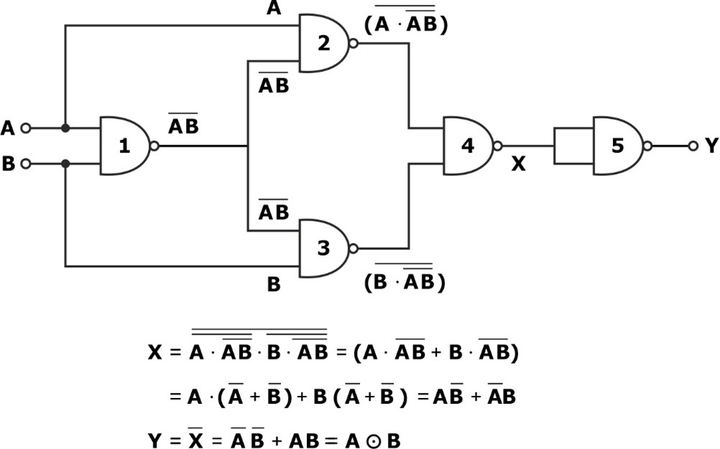
Shortcuts for the realization of logic gates are as follows:

GATES	Number of NAND Gate
NOT	1
AND	2
OR	3
EX-OR	4
EX-NOR	5

 

Important GATE Topics
Unary Operators In C	Rankine Formula
Modulus Of Rigidity	Torsion Equation
Types Of Footings	Boolean Algebra Laws
Proof Resilience	Storage Class In C
Arpanet Full Form	Number System Questions