Study notes for Trees

• Trees can be used

  • for underlying structure in decision-making algorithms
  • to represent Heaps (Priority Queues)
  • to represent B-Trees (fast access to the database)
  • for storing hierarchies in organizations
  • for file system

  Binary Tree 

  A binary tree is a tree-like structure that is rooted and in which each node has at most two children, and each child of a node is designated as its left or right child. In this kind of tree, the maximum degree of any node is at most 2. A binary tree T is defined as a finite set of elements such that

  • T is empty (called NULL tree or empty tree).
  • T contains a distinguished Node R called the root of T, and the remaining nodes of T form an ordered pair of disjoint binary trees T1 and T2.
• Node: Each data item in a tree.
• Root: First or top data item in a hierarchical arrangement.
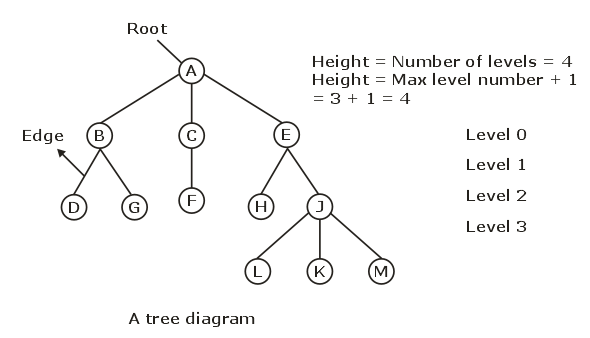
• Degree of a Node: Number of subtrees of a given node.Example: Degree of A = 3, Degree of E = 2
• Degree of a Tree: Maximum degree of a node in a tree.Example: Degree of above tree = 3
• Depth or Height: Maximum level number of a node + 1(i.e., level number of a farthest leaf node of a tree + 1).Example: Depth of above tree = 3 + 1= 4
• Non-terminal Node: Any node except root node whose degree is not zero.
• Forest: Set of disjoint trees.
• Siblings: D and G are siblings of parent Node B.
• Path: Sequence of consecutive edges from the source node to the destination node. 
• Internal nodes: All nodes that have children nodes are called internal nodes.
• Leaf nodes: Those nodes, which have no child, are called leaf nodes. 
• The depth of a node is the number of edges from the root to the node. 
• The height of a node is the number of edges from the node to the deepest leaf. 
• The height of a tree is the height of the root.

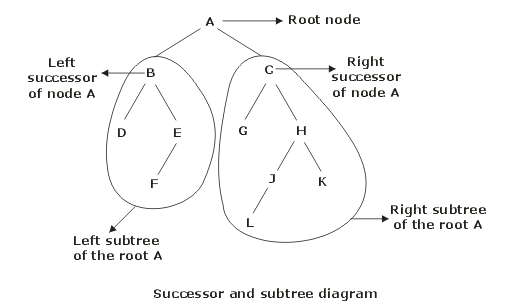
Any node N in a binary tree T has either 0, 1 or 2 successors. Level l of a binary tree T can have at most 2l nodes. The number of nodes on each level i of binary tree is at most 2i

• The number n of nodes in a binary tree of height h is at least n = h + 1 and at most n = 2h+1 – 1, where h is the depth of the tree.
• Depth d of a binary tree with n nodes >= floor(log n)
• d = floor(log N); lower bound, when a tree is a full binary tree
• d = n – 1; upper bound, when a tree is a degenerate tree

Creation of a binary tree

void insert(node ** tree, int val) {
 node *temp = NULL;
 if(!(*tree)) {
   temp = (node *)malloc(sizeof(node));
   temp->left = temp->right = NULL;
   temp->data = val;
   *tree = temp;
   return;
 }

 if(val < (*tree)->data) {
      insert(&(*tree)->left, val);
   } 
 else if(val > (*tree)->data) {
     insert(&(*tree)->right, val);
   }
 }

Search an element into binary tree

node* search(node ** tree, int val) {
 if(!(*tree)) {
   return NULL;
 }
 if(val == (*tree)->data) {
   return *tree;
  } 
 else if(val < (*tree)->data) {
    search(&((*tree)->left), val);
  } 
 else if(val > (*tree)->data){
    search(&((*tree)->right), val);
  }
 }

Delete an element from binary tree

void deltree(node * tree) {
 if (tree) {
   deltree(tree->left);
   deltree(tree->right);
   free(tree);
  }
}

If every non-terminal node in a binary tree consists of non-empty left subtree and right subtree. In other words, if any node of a binary tree has either 0 or 2 child nodes, then such tree is known as strictly binary tree or extended binary tree or 2- tree. Complete Binary Tree: A complete binary tree is a tree in which every level, except possibly the last, is filled. A complete binary tree has the following properties

• Which can have 0, 1 or 2 children.
• First, we need to fill the left node, then the right node in a level.
• We can start putting data items in the next level only when the previous level is filled.
• A complete binary tree of the height h has between 2h and 2(h+1)-1 nodes.

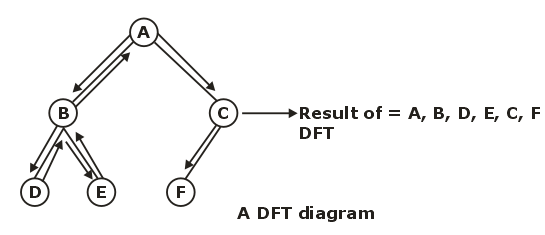
Tree Traversal: Three types of tree traversal are given below 

Preorder 

• Process the root R.
• Traverse the left subtree of R in preorder.
• Traverse the right subtree of R in preorder.

/* Recursive function to print the elements of a binary tree with preorder traversal*/
void preorder(struct btreenode *node)
{
  if (node != NULL)
  {
    printf("%d", node->data);
    preorder(node->left);
    preorder(node->right);
  }
}

Inorder

• Traverse the left subtree of R in inorder.
• Process the root R.
• Traverse the right subtree of R in inorder.

/* Recursive function to print the elements of a binary tree with inorder traversal*/
void inorder(struct btreenode *node)
{
  if (node != NULL)
  {
    inorder(node->left);   
    printf("%d", node->data);
    inorder(node->right);
  }
}

Postorder

• Traverse the left subtree of R in postorder.
• Traverse the right subtree of R in postorder.
• Process the root R.

/* Recursive function to print the elements of a binary tree with postorder traversal*/
void postorder(struct btreenode *node)
{
  if (node != NULL)
  {
    postorder(node->left);   
    postorder(node->right);
    printf("%d", node->data);
  }
}

Breadth First Traversal (BFT): The breadth-first traversal of a tree visits the nodes in the order of their depth in the tree. BFT first visits all the nodes at depth zero (i.e., root), then all the nodes at depth 1 and so on. At each depth, the nodes are visited from left to right.

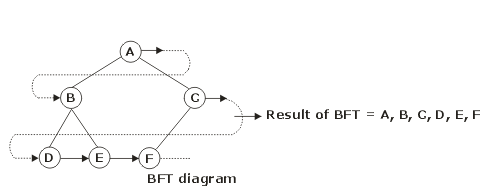
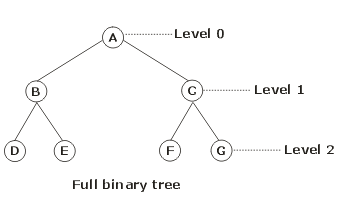
All leaves (D, E, F, G) are at depth 3 or 2, and every parent has exactly 2 children. Let a binary tree contain MAX, the maximum number of nodes possible for its height h. Then h= log(MAX + 1) –1.

The height of the Binary Search Tree equals the number of links of the path from the root node to the deepest node.

• Number of internal/leaf nodes in a full binary tree of height h2h leaves
• 2h -1 internal nodes

Expression Tree

An expression tree is a binary tree that represents a binary arithmetic expression. All internal nodes in the expression tree are operators, and leaf nodes are the operands. The expression tree will help in the precedence relation of operators. (2+3)*4 and 2+(3*4) expressions will have different expression trees.