Study notes for Queues
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Queues are an essential data structure in computer science that follows the First-In-First-Out (FIFO) principle. They play a significant role in various algorithms and are widely used in programming and system design.
In this article, we will provide you with comprehensive study notes on Queues, covering their definition, operations, types, and common applications.
Down load Formulas for GATE Computer Science Engineering – Algorithms
Table of content
Queue Definition
A queue is an abstract data type that represents a collection of elements arranged in a specific order. It follows the FIFO, meaning the element enqueued or added first will be dequeued or removed first. Think of it like a queue of people waiting in line, where the first person to join the line is the first one to be served and leave the line.
In a queue, elements are added to one end, known as the rear or tail, and removed from the other end, known as the front or head. This ordering ensures that the elements maintain their relative order. New elements are always added to the rear, and removals are performed from the front.
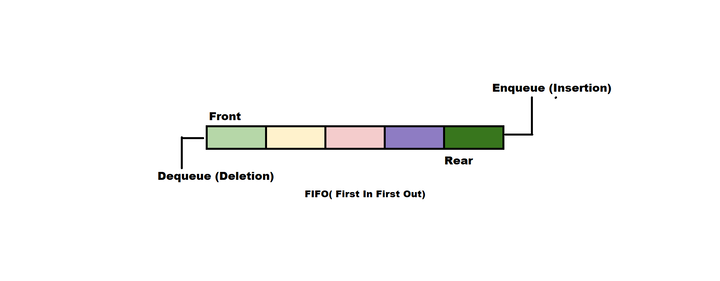
Operations on Queue
- Enqueue: This operation adds an element to the rear of the queue. It is also known as “push” or “insert.”
- Dequeue: This operation removes the element from the front of the queue. It is also known as “pop” or “delete.”
Apart from these fundamental operations, queues often have the following auxiliary operations:
- Front: The front operation retrieves the element at the front of the queue, but does not remove it.
- Rear: The rear operation retrieves the element at the rear of the queue, without removing it.
- IsEmpty: The isEmpty operation determines if the queue is empty or not. It returns true if the queue is empty, and false otherwise.
- Size: The size operation provides the count of elements currently present in the queue.
GATE Syllabus for All Engineering Branches
Queue Implementation
There are two ways of Queue Implementation:
- Static implementation which is done using Arrays
- Dynamic implementation which is done using Linked Lists
Queue Implementation With Arrays
Here’s an example of a Queue implementation with Arrays:
#define MAX_SIZE 5
typedef struct {
int queue[MAX_SIZE];
int front;
int rear;
int size;
} Queue;
void initQueue(Queue* q) {
q->front = 0;
q->rear = -1;
q->size = 0;
}
int isEmpty(Queue* q) {
return q->size == 0;
}
int isFull(Queue* q) {
return q->size == MAX_SIZE;
}
void enqueue(Queue* q, int item) {
if (isFull(q)) {
printf(“Queue is full. Unable to enqueue item.n”);
return;
}
q->rear = (q->rear + 1) % MAX_SIZE;
q->queue[q->rear] = item;
q->size++;
}
int dequeue(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty. Unable to dequeue item.n”);
return -1;
}
int item = q->queue[q->front];
q->front = (q->front + 1) % MAX_SIZE;
q->size–;
return item;
}
int peek(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty.n”);
return -1;
}
return q->queue[q->front];
}
void display(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty.n”);
return;
}
int idx = q->front;
while (idx != q->rear) {
printf(“%d “, q->queue[idx]);
idx = (idx + 1) % MAX_SIZE;
}
printf(“%dn”, q->queue[q->rear]);
}
int main() {
Queue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&queue, 30);
enqueue(&queue, 40);
display(&queue); // Output: 10 20 30 40
printf(“%dn”, dequeue(&queue)); // Output: 10
printf(“%dn”, peek(&queue)); // Output: 20
display(&queue); // Output: 20 30 40
return 0;
}
In this implementation, we define a Queue structure to hold the array, front index, rear index, and size of the queue. The initQueue function initializes the queue with appropriate values. The isEmpty and isFull functions check if the queue is empty or full, respectively. The enqueue function adds elements to the rear of the queue, and the dequeue function removes elements from the front of the queue. The peek function returns the front element without removing it. The display function prints all the elements in the queue. In the main function, we demonstrate the usage of the queue by enqueueing, dequeueing, peeking, and displaying the elements.
Queue Implementation With Linked Lists
Here’s an example of queue implementation with linked lists:
typedef struct Node {
int data;
struct Node* next;
} Node;
typedef struct {
Node* front;
Node* rear;
} Queue;
void initQueue(Queue* q) {
q->front = NULL;
q->rear = NULL;
}
int isEmpty(Queue* q) {
return q->front == NULL;
}
void enqueue(Queue* q, int item) {
Node* newNode = (Node*)malloc(sizeof(Node));
if (newNode == NULL) {
printf(“Failed to allocate memory for a new node.n”);
return;
}
newNode->data = item;
newNode->next = NULL;
if (isEmpty(q)) {
q->front = newNode;
q->rear = newNode;
} else {
q->rear->next = newNode;
q->rear = newNode;
}
}
int dequeue(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty. Unable to dequeue item.n”);
return -1;
}
Node* temp = q->front;
int item = temp->data;
q->front = q->front->next;
free(temp);
if (q->front == NULL) {
q->rear = NULL;
}
return item;
}
int peek(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty.n”);
return -1;
}
return q->front->data;
}
void display(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty.n”);
return;
}
Node* current = q->front;
while (current != NULL) {
printf(“%d “, current->data);
current = current->next;
}
printf(“n”);
}
int main() {
Queue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&queue, 30);
enqueue(&queue, 40);
display(&queue); // Output: 10 20 30 40
printf(“%dn”, dequeue(&queue)); // Output: 10
printf(“%dn”, peek(&queue)); // Output: 20
display(&queue); // Output: 20 30 40
return 0;
}
In this implementation, we define a Node structure to represent each node in the linked list. The Queue structure holds pointers to the front and rear nodes of the queue. The initQueue function initializes the queue with NULL values. The isEmpty function checks if the queue is empty. The enqueue function adds elements to the rear of the queue by creating a new node and updating the appropriate pointers. The dequeue function removes elements from the front of the queue and updates the front pointer accordingly. The peek function returns the front element without removing it. The display function prints all the elements in the queue. In the main function, we demonstrate the usage of the queue by enqueueing, dequeueing, peeking, and displaying the elements. Remember to free the allocated memory after usage to prevent memory leaks.
Types of Queues
Simple Queue
In a simple queue, elements are inserted at the rear and removed from the front.
Circular Queue
A circular queue is a variation of the simple queue in which the rear and front wrap around to the beginning of the array. It efficiently utilizes the available space and overcomes the limitation of the simple queue.
Note: A circular queue addresses the issue of wasted space in linear queues implemented as arrays. The following assumptions can be made for a circular queue:
If (Rear+1) % n == Front, then the queue is considered full.
If Front equals Rear, the queue will be empty.
Whenever a new element is inserted into the queue, the Rear is incremented by 1 using the formula Rear = (Rear + 1) % n.
Whenever an element is removed from the queue, the Front value is incremented by one using the formula Front = (Front + 1) % n.
Priority Queue
In a priority queue, each element is assigned a priority. The element with the highest priority is dequeued first. Priority queues are commonly implemented using heaps.
If elements with the same priority occur, they are served according to their order in the queue.
Deque
A deque (Double Ended Queue) is a queue that allows insertion and deletion at both ends.
Double Ended Queue
A Double Ended Queue (deque) is a data structure that allows insertion and removal of elements from both ends, front and rear. It is sometimes referred to as a “deque” (pronounced “deck”). This data structure combines the features of both stacks and queues, providing flexibility in managing elements.
Applications of Queues
Queues find applications in various fields, including but not limited to:
- Breadth-First Search (BFS): Queue data structure is extensively used in the BFS algorithm to traverse and explore graph or tree structures. In BFS, nodes are visited in levels, starting from the root node and moving towards its neighbors. The queue is used to store the nodes in the order they are visited, ensuring that nodes at the same level are processed before moving to the next level.
- CPU Scheduling: Queues are crucial in CPU scheduling algorithms, such as Round Robin, First-Come-First-Serve, and Priority Scheduling. Processes waiting to be executed are stored in a queue, and the scheduler selects the next process to run based on the scheduling algorithm.
- Handling of interrupts in real-time systems: Interrupts are signals sent by hardware devices or software events that require immediate attention from the processor. Queues are used to manage interrupts in real-time systems, allowing the system to handle them in a timely and orderly manner. Interrupts are placed in a queue and processed based on their priority or arrival time.
- Routing Algorithms: Queues are employed in various routing algorithms, such as packet switching networks and network protocols like TCP/IP. Queues are used to hold packets or data packets temporarily before they are forwarded to the next node or destination.
- Computation of shortest paths: Algorithms like Dijkstra’s algorithm and Bellman-Ford algorithm, used to find the shortest path in a graph, utilize queues. The queue is used to hold the neighboring nodes to be explored during the process of finding the shortest path.
- Computation of a cycle in a graph: Queues can be used to determine if a cycle exists in a graph. By performing a breadth-first search (BFS) or depth-first search (DFS) on the graph and using a queue to store the nodes being explored, it is possible to detect cycles by checking if a node is visited again before its exploration is complete.
Important Points to Remember
- Queues can be implemented using arrays, linked lists, or other dynamic data structures.
- Circular queues provide efficient space utilization and support queue operations effectively.
- Priority queues are commonly implemented using binary heaps or other efficient data structures to ensure efficient retrieval of the highest priority element.
- Queues can be implemented using different programming languages, including C, C++, Java, and Python.
- Familiarize yourself with the time complexities of queue operations to analyze the efficiency of algorithms that use queues.
Some examples on Queue:
- Reversing the Queue Q using the Stack S
#define MAX_SIZE 5
typedef struct {
int queue[MAX_SIZE];
int front;
int rear;
int size;
} Queue;
void initQueue(Queue* q) {
q->front = 0;
q->rear = -1;
q->size = 0;
}
int isEmpty(Queue* q) {
return q->size == 0;
}
int isFull(Queue* q) {
return q->size == MAX_SIZE;
}
void enqueue(Queue* q, int item) {
if (isFull(q)) {
printf(“Queue is full. Unable to enqueue item.n”);
return;
}
q->rear = (q->rear + 1) % MAX_SIZE;
q->queue[q->rear] = item;
q->size++;
}
int dequeue(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty. Unable to dequeue item.n”);
return -1;
}
int item = q->queue[q->front];
q->front = (q->front + 1) % MAX_SIZE;
q->size–;
return item;
}
void display(Queue* q) {
if (isEmpty(q)) {
printf(“Queue is empty.n”);
return;
}
int idx = q->front;
while (idx != q->rear) {
printf(“%d “, q->queue[idx]);
idx = (idx + 1) % MAX_SIZE;
}
printf(“%dn”, q->queue[q->rear]);
}
void reverseQueue(Queue* q) {
if (isEmpty(q))
return;
int stack[MAX_SIZE];
int top = -1;
// Dequeue each element from the queue and push it onto the stack
while (!isEmpty(q)) {
int item = dequeue(q);
stack[++top] = item;
}
// Pop each element from the stack and enqueue it back into the queue
while (top >= 0) {
int item = stack[top–];
enqueue(q, item);
}
}
int main() {
Queue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&queue, 30);
enqueue(&queue, 40);
printf(“Original Queue: “);
display(&queue); // Output: 10 20 30 40
printf(“Reversed Queue: “);
reverseQueue(&queue);
display(&queue); // Output: 40 30 20 10
return 0;
}
Here, we have added the reverseQueue function to reverse the elements in the queue using a stack. The reverseQueue function dequeues each element from the queue and pushes it onto the stack. Then, it pops each element from the stack and enqueues it back into the queue. Finally, we demonstrate the usage of the reverseQueue function by reversing the elements in the queue and displaying the result.
Implementation of Stack Using two Queues
Method 1:
// Structure representing a queue
typedef struct {
int *arr; // Array to store elements
int front; // Front of the queue
int rear; // Rear of the queue
int size; // Current size of the queue
int capacity; // Maximum capacity of the queue
} Queue;
// Create a new queue
Queue* createQueue(int capacity) {
Queue* queue = (Queue*)malloc(sizeof(Queue));
queue->arr = (int*)malloc(capacity * sizeof(int));
queue->front = 0;
queue->rear = -1;
queue->size = 0;
queue->capacity = capacity;
return queue;
}
// Check if the queue is empty
int isEmpty(Queue* queue) {
return queue->size == 0;
}
// Check if the queue is full
int isFull(Queue* queue) {
return queue->size == queue->capacity;
}
// Enqueue an element to the queue
void enqueue(Queue* queue, int item) {
if (isFull(queue)) {
printf(“Queue is full. Cannot enqueue.n”);
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->arr[queue->rear] = item;
queue->size++;
}
// Dequeue an element from the queue
int dequeue(Queue* queue) {
if (isEmpty(queue)) {
printf(“Queue is empty. Cannot dequeue.n”);
return -1;
}
int item = queue->arr[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size–;
return item;
}
// Get the top element of the queue (without removing it)
int front(Queue* queue) {
if (isEmpty(queue)) {
printf(“Queue is empty.n”);
return -1;
}
return queue->arr[queue->front];
}
// Structure representing a stack using two queues
typedef struct {
Queue* q1; // Primary queue
Queue* q2; // Secondary queue
} Stack;
// Create a new stack
Stack* createStack(int capacity) {
Stack* stack = (Stack*)malloc(sizeof(Stack));
stack->q1 = createQueue(capacity);
stack->q2 = createQueue(capacity);
return stack;
}
// Push an element onto the stack
void push(Stack* stack, int item) {
if (isFull(stack->q1)) {
printf(“Stack is full. Cannot push.n”);
return;
}
enqueue(stack->q1, item);
}
// Pop an element from the stack
int pop(Stack* stack) {
if (isEmpty(stack->q1)) {
printf(“Stack is empty. Cannot pop.n”);
return -1;
}
while (stack->q1->size > 1) {
enqueue(stack->q2, dequeue(stack->q1));
}
int item = dequeue(stack->q1);
Queue* temp = stack->q1;
stack->q1 = stack->q2;
stack->q2 = temp;
return item;
}
// Get the top element of the stack (without removing it)
int top(Stack* stack) {
if (isEmpty(stack->q1)) {
printf(“Stack is empty.n”);
return -1;
}
while (stack->q1->size > 1) {
enqueue(stack->q2, dequeue(stack->q1));
}
int item = front(stack->q1);
enqueue(stack->q2, dequeue(stack->q1));
Queue* temp = stack->q1;
stack->q1 = stack->q2;
stack->q2 = temp;
return item;
}
// Check if the stack is empty
int isStackEmpty(Stack* stack) {
return isEmpty(stack->q1);
}
// Check if the stack is full
int isStackFull(Stack* stack) {
return isFull(stack->q1);
}
// Main function
int main() {
Stack* stack = createStack(5);
push(stack, 10);
push(stack, 20);
push(stack, 30);
printf(“Top element: %dn”, top(stack));
printf(“Popped element: %dn”, pop(stack));
printf(“Popped element: %dn”, pop(stack));
push(stack, 40);
push(stack, 50);
printf(“Top element: %dn”, top(stack));
printf(“Popped element: %dn”, pop(stack));
printf(“Is stack empty? %sn”, isStackEmpty(stack) ? “Yes” : “No”);
printf(“Is stack full? %sn”, isStackFull(stack) ? “Yes” : “No”);
return 0;
}
In this implementation, two queues are used to simulate a stack. The push operation enqueues elements into the primary queue (q1), and the pop operation dequeues elements from q1 by transferring all but the last element to the secondary queue (q2). The last element is then dequeued from q1, and the queues are swapped, making q2 the new primary queue.
The implementation includes functions to create a stack, push elements, pop elements, get the top element without removing it, and check if the stack is empty or full.
The main function demonstrates the usage of the stack by pushing and popping elements and checking the top element and stack status.
Method 2:
// Structure representing a queue
typedef struct {
int *arr; // Array to store elements
int front; // Front of the queue
int rear; // Rear of the queue
int size; // Current size of the queue
int capacity; // Maximum capacity of the queue
} Queue;
// Create a new queue
Queue* createQueue(int capacity) {
Queue* queue = (Queue*)malloc(sizeof(Queue));
queue->arr = (int*)malloc(capacity * sizeof(int));
queue->front = 0;
queue->rear = -1;
queue->size = 0;
queue->capacity = capacity;
return queue;
}
// Check if the queue is empty
int isEmpty(Queue* queue) {
return queue->size == 0;
}
// Check if the queue is full
int isFull(Queue* queue) {
return queue->size == queue->capacity;
}
// Enqueue an element to the queue
void enqueue(Queue* queue, int item) {
if (isFull(queue)) {
printf(“Queue is full. Cannot enqueue.n”);
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->arr[queue->rear] = item;
queue->size++;
}
// Dequeue an element from the queue
int dequeue(Queue* queue) {
if (isEmpty(queue)) {
printf(“Queue is empty. Cannot dequeue.n”);
return -1;
}
int item = queue->arr[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size–;
return item;
}
// Get the front element of the queue (without removing it)
int front(Queue* queue) {
if (isEmpty(queue)) {
printf(“Queue is empty.n”);
return -1;
}
return queue->arr[queue->front];
}
// Structure representing a stack using two queues
typedef struct {
Queue* q1; // Primary queue
Queue* q2; // Secondary queue
} Stack;
// Create a new stack
Stack* createStack(int capacity) {
Stack* stack = (Stack*)malloc(sizeof(Stack));
stack->q1 = createQueue(capacity);
stack->q2 = createQueue(capacity);
return stack;
}
// Push an element onto the stack
void push(Stack* stack, int item) {
if (isFull(stack->q1)) {
printf(“Stack is full. Cannot push.n”);
return;
}
enqueue(stack->q1, item);
}
// Pop an element from the stack
int pop(Stack* stack) {
if (isEmpty(stack->q1)) {
printf(“Stack is empty. Cannot pop.n”);
return -1;
}
while (stack->q1->size > 1) {
enqueue(stack->q2, dequeue(stack->q1));
}
int item = dequeue(stack->q1);
Queue* temp = stack->q1;
stack->q1 = stack->q2;
stack->q2 = temp;
return item;
}
// Get the top element of the stack (without removing it)
int top(Stack* stack) {
if (isEmpty(stack->q1)) {
printf(“Stack is empty.n”);
return -1;
}
return front(stack->q1);
}
// Check if the stack is empty
int isStackEmpty(Stack* stack) {
return isEmpty(stack->q1);
}
// Check if the stack is full
int isStackFull(Stack* stack) {
return isFull(stack->q1);
}
// Main function
int main() {
Stack* stack = createStack(5);
push(stack, 10);
push(stack, 20);
push(stack, 30);
printf(“Top element: %dn”, top(stack));
printf(“Popped element: %dn”, pop(stack));
printf(“Popped element: %dn”, pop(stack));
push(stack, 40);
push(stack, 50);
printf(“Top element: %dn”, top(stack));
printf(“Popped element: %dn”, pop(stack));
printf(“Is stack empty? %sn”, isStackEmpty(stack) ? “Yes” : “No”);
printf(“Is stack full? %sn”, isStackFull(stack) ? “Yes” : “No”);
return 0;
}
This implementation is similar to the previous one, but with a slight modification in the pop function. Rather than swapping the queues after each pop operation, we simply transfer all elements except the last one from q1 to q2. After that, we dequeue and return the last element from q1. This approach eliminates the need to swap the queues, making the code slightly simpler.
Applications of Queue
BFS using Queue
Breadth-First Search (BFS) is a graph traversal algorithm that explores all the vertices of a graph in breadth-first order, i.e., it visits all the vertices at the same level before moving on to the next level. It can be implemented using a queue to store the vertices to be visited. Here’s an outline of how BFS can be implemented using a queue:
- Create a queue and a visited array to keep track of visited vertices.
- Enqueue the starting vertex into the queue and mark it as visited.
- While the queue is not empty, do the following:
- Dequeue a vertex from the queue and process it.
- Explore all the adjacent vertices of the dequeued vertex that have not been visited.
- Enqueue each unvisited adjacent vertex into the queue and mark it as visited.
- Repeat step 3 until the queue becomes empty.
#define MAX_VERTICES 100
// Queue implementation
typedef struct {
int arr[MAX_VERTICES];
int front;
int rear;
} Queue;
void initQueue(Queue* queue) {
queue->front = -1;
queue->rear = -1;
}
bool isEmpty(Queue* queue) {
return (queue->front == -1 && queue->rear == -1);
}
void enqueue(Queue* queue, int item) {
if (isEmpty(queue)) {
queue->front = 0;
queue->rear = 0;
} else {
queue->rear = (queue->rear + 1) % MAX_VERTICES;
}
queue->arr[queue->rear] = item;
}
int dequeue(Queue* queue) {
int item = queue->arr[queue->front];
if (queue->front == queue->rear) {
queue->front = -1;
queue->rear = -1;
} else {
queue->front = (queue->front + 1) % MAX_VERTICES;
}
return item;
}
// BFS algorithm using a queue
void bfs(int graph[MAX_VERTICES][MAX_VERTICES], int vertices, int start) {
bool visited[MAX_VERTICES] = { false };
Queue queue;
initQueue(&queue);
enqueue(&queue, start);
visited[start] = true;
while (!isEmpty(&queue)) {
int vertex = dequeue(&queue);
printf(“%d “, vertex);
for (int i = 0; i < vertices; i++) {
if (graph[vertex][i] && !visited[i]) {
enqueue(&queue, i);
visited[i] = true;
}
}
}
}
int main() {
int vertices, edges;
printf(“Enter the number of vertices: “);
scanf(“%d”, &vertices);
printf(“Enter the number of edges: “);
scanf(“%d”, &edges);
int graph[MAX_VERTICES][MAX_VERTICES] = { { 0 } };
printf(“Enter the edges (u v):n”);
for (int i = 0; i < edges; i++) {
int u, v;
scanf(“%d %d”, &u, &v);
graph[u][v] = 1;
graph[v][u] = 1;
}
int startVertex;
printf(“Enter the starting vertex: “);
scanf(“%d”, &startVertex);
printf(“BFS traversal starting from vertex %d: “, startVertex);
bfs(graph, vertices, startVertex);
return 0;
}
This C code prompts the user to enter the number of vertices and edges in the graph. It then takes input for the edges and builds an adjacency matrix representation of the graph. Finally, the code asks for the starting vertex and performs a BFS traversal starting from that vertex, printing the traversal order.
Formulas for GATE Computer Science Engineering – Algorithms
Also Read:



