What is Consensus Theorem?
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Consensus Theorem is one of the approaches for computing the Blake canonical form of formula in Boolean algebra. Including the consensus term in a digital logic circuit helps reduce race concerns. The consensus theorem is one of the most powerful theorems in digital electronics for Boolean function reduction.
Archie Blake established the consensus theorem in 1937 in relation to the Blake canonical form. Samson and Mills rediscovered it in 1954, and Quine in 1955. Quine created the phrase “consensus”. Robinson used it for clauses as the foundation of his “resolution principle” in 1965. Here, we will state and prove the consensus theorem along with its examples, and truth table.
Download Formulas for GATE Mechanical Engineering-Engineering Mechanics
Table of content
What is the Consensus Theorem?
In Digital Electronics, the redundancy theorem is utilized as a Boolean algebra technique. It is sometimes referred to as the Consensus Theorem. The following conditions must be met before using the Redundancy theorem:
- The equation must have three variables.
- Each variable is repeated twice.
- One variable must be present in the complemented form.
Consensus Theorem Proof
Consider the three variables X, Y, and Z. The expression is as follows:
O = XY + YZ + X’Z
We can prove the Consensus theorem as follows:
O = XY + YZ . 1 + X’Z
O = XY + YZ(X + X’) + X’Z
O = XY + XYZ + X’YZ + X’Z
O = XY + X’Z
Another method to prove the Consensus theorem by the Karnaugh map is as follows:
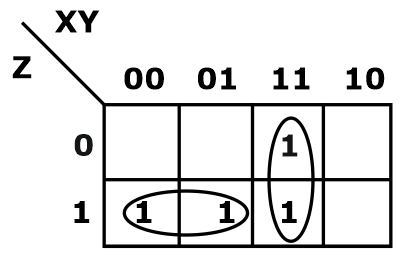
The minimized expression is:
O = XY + X’Z
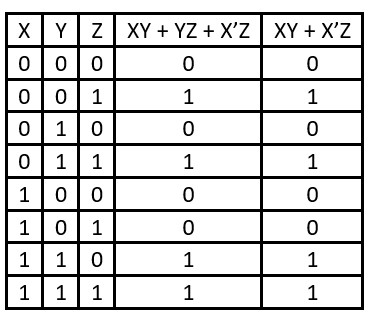
Consensus Theorem Truth Table
The truth table for the consensus theorem which is having three variables X, Y, and Z. The consensus theorem gives the output high when the Z variable is high or when both X and Y variables are input high.
Examples of Consensus Theorem
The Boolean expression F = AB + BC’ + AC. Identity whether we can apply the Consensus theorem.
In the given expression, we first check the condition for the Consensus theorem as described above:
- The given expression has three variables: A, B, and C.
- Every variable is repeated twice in the expression.
- The variable C is present in the complement form.
As all the conditions are verified so we can apply the consensus theorem. We can write just the terms containing complemented variables (i.e., C) and leave out the Redundancy term (i.e., AB) after using the Redundancy theorem.
F = BC’ + AC
The Boolean expression F = (A + B). (B + C) + (A’ + C). Identity whether we can apply the Consensus theorem.
In the given expression, we first check the condition for the Consensus theorem as described above:
- The given expression has three variables: A, B, and C.
- Every variable is repeated twice in the expression.
- The variable C is present in the complement form.
As all the conditions are verified so we can apply the consensus theorem. We can write just the terms containing complemented variables (i.e., A) and leave out the Redundancy term (i.e., B + C) after using the Redundancy theorem.
F = (A + B).(A’ + C)
| Important Topics for Gate Exam | |
| Brittle Material | Capacitors in Parallel |
| Capacitors in Series | Carnot Cycle |
| Cement Test | Clamping Circuit |
| Clipping Circuit | CMOS Fabrication |
| CMOS Converter | Column Base |


