Study Notes on Binary Heaps and Heap Sort
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The binary heap data structure is an array that can be viewed as a complete binary tree. Each node of the binary tree corresponds to an element of the array. The array is filled on all levels except possibly lowest (the lowest level is filled in left to right order and need not be complete).
Table of content
There are two types of heap trees: Max heap tree and Min heap tree.
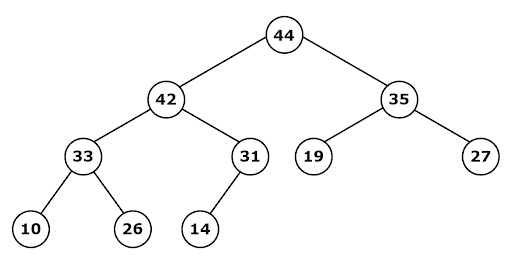
1. Max heap: In a heap, for every node i, the value of a node is greater than or equal to the value of its children.
A[PARENT (i)] ≥ A[i]. Thus, the largest element in a heap is stored at the root.
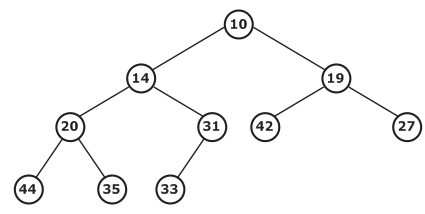
2. Min heap: In a heap, for every node i, the value of a node is less than or equal to the value of its children.
A[PARENT (i)]≤ A[i]. Thus, the smallest element in a heap is stored at the root.
The root of the tree A[1] and given index i of a node, the indices of its parent, left child, and right child can be computed as follows:
- PARENT (i): Parent of node i is at the floor(i/2)
- LEFT (i): Left child of node i is at 2i
- RIGHT (i): Right child of node i is at (2i + 1)
Since a heap is a complete binary tree, it has the smallest possible height. A heap with N nodes always has O(log N) height. A heap is a useful data structure for removing the object with the highest (or lowest) priority. A common use of a heap is to implement a priority queue.
Heapify: Heapify is a procedure for manipulating heap data structures. It is given an array A and index i into the array. The subtree rooted at the children of A[i] are heap, but node A[i] itself may hamper the property of heap. A[i] < A[2i] or A[i] < A[2i +1]. The ‘Heapify’ procedure employes the tree rooted at A[i] so that it can become a heap.
Heapify (A, i)
- l ← left [i]
- r ← right [i]
- if l ≤ heap-size [A] and A[l] > A[i]
- then largest ← l
- else largest ← i
- if r ≤ heap-size [A] and A[i] > A[largest]
- then largest ← r
- if largest ≠ i
- then exchange A[i] ↔ A[largest]
- Heapify (A, largest)
The time complexity: O(log n)
Building a Heap: Heapify procedure can be applied in a bottom-up manner to convert an array A[1 . . n] into a heap or binary heap. Since all the elements in the subarray A[⎣n/2⎦+1 . . n] are leaves, then the procedure Build_Heap went to the remaining nodes of the tree and ran the ‘Heapify’ algorithm/procedure on each node. Processing nodes in the bottom-up order guarantee that the subtree rooted at children are heap before ‘Heapify’ is run at their parent.
Build_Heap (A)
- heap-size (A) ← length [A]
- For i ← floor(length[A]/2) down to 1 do
- Heapify (A, i)
The time complexity of the Build_Heap algorithm is: O(n) Heap of height h has the minimum number of elements when it has just one node at the lowest level.
Minimum nodes of a heap of a height h: The levels above the lowest level form a complete binary tree of height h -1 and 2h -1 nodes. Hence the minimum number of nodes possible in a heap of height h is 2h nodes.
Maximum nodes of the heap of a height h: Heap of height h has the maximum number of elements when its lowest level is filled. In this case, the given heap is a complete binary tree of height h that has (2h+1 -1) nodes.
For Min heap tree of n-elements:
- Insertion of an element: O(log n)
- Delete minimum element: O(log n)
- Remove an element: O(log n)
- Find minimum element: O(1)
DecreaseKey(p,d) operation on heap:
- This operation lowers the value of the element at position p by a positive amount d.
- It is used to increase the priority of an element.
- We have to find a new position of the element according to its new priority by percolating up.
IncreaseKey(p,d) operation on heap:
- This operation increases the value of the element at position p by a positive amount d.
- It is used to decrease the priority of an element.
- We have to find a new position of the element according to its new priority by percolating down.
Remove(p) operation on the heap:
- With this operation, an element p is removed from the queue.
- This is done in two steps: Assigning the highest priority to p – percolate p up to the root.
- Deleting the element in the root and filling the hole by percolating down the last element in the queue.
Heap Sort: The heap sort combines the best of both merge sort and insertion sort. Like, merge sort, the worst-case time of heap sort is O(n log n), and like insertion sort, heap sort sorts in place.
- Given an array of n elements, first, we build the heap.
- The largest element is at the root, but its position in the sorted array should be at last. So, swap the root with the last element and heapify the tree with the remaining n-1 elements.
- We have placed the highest element in its correct position. We left with an array of n-1 elements. Repeat the same of these remaining n-1 elements to place the next largest element in its correct position.
- Repeat the above step till all elements are placed in their correct positions.
heapsort(A) {
BUILD_HEAP (A);
for (i = length (A); i>=2; i–){
exchange (A[1], A[i]);
heap-size [A] = heap-size [A] – 1;
Heapify (A, 1);
}
}
(OR)
heapsort(A) {
BUILD_HEAP (A);
heapsize ← heap-size[A];
for (i = length (A); i>=2; i–){
A[heapsize] = Heap-Extract-Max (A);
heap-size [A] = heap-size [A] – 1;
}
}
That’s all for the heap trees.
Click Here to Avail GATE CSE Test Series!
Thanks
#DreamStriveSucceed


