Shear Stress

Bending and Shear Stress

Bending Moments and Shear Stress Distribution

Bending stress and shear stress distribution are classified in the following groups

Bending Moment in Beam:

Transverse loads or lateral loads: Forces or moments having their vectors perpendicular to the axis of the bar.

Classification of structural members.

• Axially loaded bars :-Loaded in perpendicular dimension along the axis of bar. Supports forces having their vectors directed along the axis of the bar.
• Bar in tension:- Supports torques having their moment vectors directed along the axis to generate a force in the outward direction
• Beams :- Subjected to lateral loads.Beams undergo bending (flexure) because of lateral loads.

When beam is subjected to a bending moment or bent there are induced longitudinal or bending stress in cross-section.

Note that a positive bending moment M causes negative (compressive) stress above the neutral axis and positive ( tensile) stress below the neutral axis 

Equation of Pure Bending:

Assumptions:

1. The material of the beam is homogeneous and isotropic.
2. Young's Modulus of Elasticity value is the same in tension and compression.
3. The transverse sections, which were plane before bending, remain plane after bending also.
4. The beam is initially straight, and all longitudinal filaments bend into circular arcs with a common centre of curvature.
5. The radius of curvature is large as compared to the dimensions of the cross-section.
6. Each layer of the beam is free to expand or contract, independently of the layer, above or below it.

At the neutral axis, there is no stress of any kind. At one side of the neutral axis, there are compressive stresses and on the other side , there are tensile stresses.

Modulus of Section:

Elastic section modulus is defined as Z(S) = I / y, where I is the second moment of area (or Izz moment of inertia) and y is the distance from the neutral axis to any given fibre.

Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members.

Rectangular section :

Modulus of section :

Circular section :

Modulus of section :

Beams of uniform strength:

• The beam is said to be in uniform strength if the maximum bending stress is constant across the varying section along its length.
• Generally, beams are having the uniform cross-section throughout their length. When a beam is loaded, there is a variation in bending moment from section to section along the length. The stress in extreme outer fibre (top and bottom) also varies from section to section along their length. The extreme fibers can be loaded to the maximum capacity of permissible stress (say p_max), but they are loaded to less capacity. Hence, in beams of the uniform cross section there is a considerable waste of materials
• When a beam is suitably designed such that the extreme fibers are loaded to the maximum permissible stress p_max by varying the cross section it will be known as a beam of uniform strength.

Shearing Stress

Shearing stress on a layer JK of beam at distance y from neutral axis.

Where,

V = Shearing force

 First moment of area

Shear stress in Rectangular Beam

Suppose, we have to determine the shear stress at the longitudinal layer having y distance from neutral axis.

Circular Beam

Centre of gravity of semi-circle lies at distance from centre or base line. As it is symmetrical above neutral axis, hence at neutral axis shear stress will be maximum.

Shears Stress in Hollow Circular Cross-Section

In hollow circular cross-section, if we have to calculate τ at neutral axis by the formula

Shear Stress in Triangular Section

In a triangular cross-section, if we have to calculate τ at neutral axis, then in formula

Shear Stress in I-section

Combined Stress

Bending stress and shear stress distribution are classified in the following groups

Bending Moment in Beam:

Transverse loads or lateral loads: Forces or moments having their vectors perpendicular to the axis of the bar.

Classification of structural members

• Axially loaded bars: Supports forces having their vectors directed along the axis of the bar.
• Bar in tension: Supports torques having their moment vectors directed along the axis.
• Beams
  • Subjected to lateral loads.
  • Beams undergo bending (flexure) because of lateral loads.

When beam is subjected to a bending moment or bent there are induced longitudinal or bending stress in cross-section.

Bending Stress in beam:

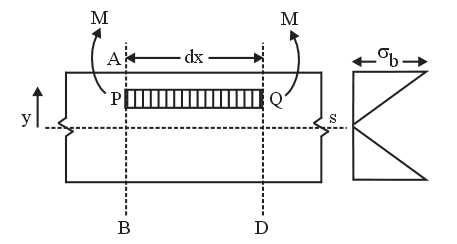
• I is Moment of Inertia about Neutral Axis
• Note that a positive bending moment M causes negative (compressive) stress above the neutral axis and positive ( tensile) stress below the neutral axis 

Equation of Pure Bending:

Assumptions:

1. The material of the beam is homogeneous and isotropic.
2. The value of Young's Modulus of Elasticity is same in tension and compression.
3. The transverse sections which were plane before bending, remain plane after bending also, that means strain diagram is linear.
4. The beam is initially straight and all longitudinal filaments bend into circular arcs with a common centre of curvature.
5. The radius of curvature is large as compared to the dimensions of the cross-section.
6. Each layer of the beam is free to expand or contract, independently of the layer, above or below it.

Modulus of Section

• Elastic section modulus is defined as Z(S) = I / y, where I is the second moment of area (or Izz moment of inertia) and y is the distance from the neutral axis to any given fibre.
• Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members.

• Rectangular section:
  • Modulus of the section :                                       
• Circular section :
  • Modulus of section :

Beams of uniform strength

• The beam is said to be in uniform strength if the maximum bending stress is constant across the varying section along its length.
• Generally, beams are having the uniform cross-section throughout their length. When a beam is loaded, there is a variation in bending moment from section to section along the length. The stress in extreme outer fibre (top and bottom) also varies from section to section along their length. The extreme fibres can be loaded to the maximum capacity of permissible stress (say p_max), but they are loaded to less capacity. Hence, in beams of uniform cross section, there is a considerable waste of materials
• When a beam is suitably designed such that the extreme fibres are loaded to the maximum permissible stress p_max by varying the cross section it will be known as a beam of uniform strength.

Shearing Stress

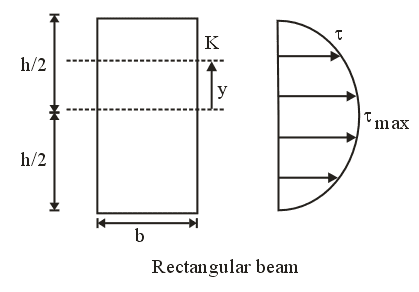
• Shearing stress on a layer JK of beam at distance y from neutral axis.

Where,

• V = Shearing force
•  First moment of area

Shear stress in Rectangular Beam

• Suppose, we have to determine the shear stress at the longitudinal layer having y distance from neutral axis.

Circular Beam

• Centre of gravity of semi-circle lies at distance from centre or base line. As it is symmetrical above neutral axis, hence at neutral axis shear stress will be maximum.

Shears Stress in Hollow Circular Cross-Section

• In hollow circular cross-section, if we have to calculate τ at neutral axis by the formula

Shear Stress in Triangular Section

• In a triangular cross-section, if we have to calculate τ at neutral axis, then in formula

Shear Stress in I-section

Combined Stresses

Definitions of Direct, Bending & Shear Stress

1. Stress due to Twisting Moment + Bending Moment

• Equivalent Torsional Moment:

        The equivalent torsional moment is defined as the torsional moment, which when acting alone, will produce the same torsional shear stress
         in the shaft as under the combined action of bending moment (M_b) and torsional moment (M_t)

            Equivalent torsional moment= T_e=
                                                                             

• Equivalent Bending Moment:

        The equivalent Bending moment is defined as the bending moment, which when acting alone, will produce the same bending stresses (tensile and compressive) in the shaft as under the combined action of bending moment (M_b) and torsional moment (M_t).

Equivalent bending moment=                                                                             

Example:- A shaft of diameter 8 cm is subjected to a bending moment of 3000 Nm and a twisting moment of 4000 Nm. The maximum normal stress induced in the shaft is equal to

Solution:-

2. Stress due to Axial Load + Bending Moment

        Suppose a beam under direct compressive and bending load as shown in the diagram. where A=Area,

        y=distance of extreme fiber from Neutral axis and I= moment of Inertia

so total stress at upper fiber

= Direct compressive stress + tensile stress due to a bending load

=(-σ)+σ_b

=   

Same for lower extreme fiber

= Direct compressive stress + Compressive stress due to bending load

=(-σ)+(-σ_b)

=

Example- For the component loaded with a force F as shown in the figure, the axial stress at the corner point P is

Solution:-

At point P two types of stress are acting, bending & axial tensile load
So, bending stress =

Axial tensile stress =

Total axial stress at P = σ_b + σ_a

Thanks

All the Best