Laplace Transform: It is an integral transformation of a function f(t) from the time domain into the complex frequency domain F(s).
Laplace transform can be used to transform the time domain circuits into S domain circuits to simplify the solution of integral differential equations to the manipulation of a set of algebraic equations.
If f(t) is the time domain function then its Laplace transform is denoted by F(s) and is defined by the equation.
where s is complex frequency variable.
s=σ + jω; where σ is attenuation constant (damping factor, and ω is angular frequency.

Circuit Analysis using Laplace and Inverse Laplace transform
Properties of Laplace Transform
Linearity- t-domain: L[K1f1(t) + K2f2(t)]
- s-domain: [K1f1(s) + K2f2(s)]
- t-domain:

- s-domain: snf(s) – sn–1f(0) – sn–2f′(0) – sn–3f′(0)…..
- t-domain:

- s-domain:
![]()
- t-domain: L[f(at)]
- s-domain:
![]()
- t-domain: L[f(t – a)]
- s-domain: e–as f(s)
- t-domain: L[e–at f(t)]
- s-domain: f(s + a)
- t-domain: L[f1(t) × f2(t)]
- s-domain: f1(s) ∙ f2(s)
- t-domain:
- s-domain:
![]()
- t-domain:
- s-domain:
![]()
Laplace Transform of Periodic Function

where, f1(t) = Function over one time period, and f(t) = Periodic function with time period T.
Functions & Laplace transform- Constant function (1) or Unit step function (u(t)) : Laplace Transform is 1/s
- Unit step function shifted / delayed by T ( U(t – T) ): Laplace Transform is (e–sT)/s
- Unit impulse ( δ(t) ): Laplace Transform is 1
- Exponential function ( eat ): Laplace Transform: 1/(s – a)
- Exponential function (e–at ): Laplace Transform is 1/(s + a)
- Sine function ( sin ωt ): Laplace Transform is ω/(s2 + ω2)
- Cosine function ( cos ωt ): Laplace Transform is s/(s2 + ω2)
- Damped Sine ( e–at sin ωt ): Laplace Transform is ω/((s+a)2 + ω2)
- Damped Cosine ( e–at sin ωt ): Laplace Transform is (s+a) /((s+a)2 + ω2)
- Ramp function ( tn (n = 1, 2, 3,….) ): Laplace Transform is
- Unit ramp function ( t ): Laplace Transform is 1/s2
- Damped sine function ( e–at sin ωt ): Laplace Transform is

- Damped cosine function ( e–at cos ωt ): Laplace Transform is

- Damped cosine function ( e–at tn ): Laplace Transform is

- Differentiation theorem (
 ) : Laplace Transform is sF(s) – f(0 –)
) : Laplace Transform is sF(s) – f(0 –)
- Integration theorem (
 ) Laplace Transform is
) Laplace Transform is
- Hyperbolic sine function ( sin h ωt ): Laplace Transform
- Hyperbolic cosine function ( cos h ωt ): Laplace Transform is
- Damped hyperbolic sine function ( e–at sin h ωt ): Laplace Transform is

- Damped hyperbolic cosine function ( e–at cos h ωt ): Laplace Transform is

- Initial value theorem: Laplace Transform is
![]()
- Final value theorem: Laplace Transform is
![]()
- Shifting theorem f(t ± a): Laplace Transform is e±as F(s)
Laplace Transform of a Periodic Function
f(t + nt) = f(t), where n is positive or negative integer.
![]()
where, F1(s) is the Laplace transform of the first cycle of the periodic function.

Analysis of Basic elements (R,L and C): Let I = I(s) be the Laplace transform of i= i (t).
Capacitor:
Resistor:



 )
)


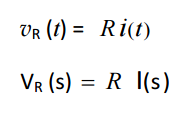





Comments
write a comment