- Home/
- GATE ELECTRICAL/
- GATE EE/
- Article
Fourier Transform and its Properties Study notes
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Fourier Transform is a powerful mathematical tool widely used in signal processing, mathematics, and various engineering disciplines. It allows us to analyze signals and functions in the frequency domain, providing insights into the frequency components that make up a given signal. Developed by Joseph Fourier, the transform converts a time-domain signal into its equivalent representation in the frequency domain, showing how different sinusoidal components contribute to the signal’s overall behaviour. By doing so, the Fourier Transform helps to reveal hidden patterns, identify dominant frequencies, and facilitate filtering and noise reduction processes.
The study of the Fourier Transform goes beyond its basic definition and delves into its remarkable properties, which make it an indispensable tool in various applications. Some of the key properties include linearity, time and frequency shifting, convolution, and duality. Linearity allows us to analyze complex signals by breaking them down into simpler components. Time and frequency shifting properties enable the analysis of signals with respect to time and frequency shifts. The convolution property allows us to analyze the output of the system by convolving the input and impulse response. Lastly, duality is a fundamental concept that establishes the reciprocity between the time and frequency domains. Understanding these properties equips engineers and researchers with a powerful set of tools to tackle a wide array of challenges in signal processing and beyond.
Download Formulas for GATE Electrical Engineering – Digital Circuits
Table of content
Fourier Transform
Fourier transform is a transformation technique which transforms non-periodic signals from the continuous-time domain to the corresponding frequency domain. The Fourier transform of a continuous-time non-periodic signal x(t) is defined as
where X(jω) is the frequency domain representation of the signal x(t) and F denotes the Fourier transformation. The variable ‘ ω’ is the radian frequency in rad/sec. Sometimes X(jω) is also written as X(ω).
If the frequency is represented in terms of cyclic frequency f (in Hz), then the above equation is written as
Formulas for GATE Electrical Engineering – Power Systems
Note:
The signal x(t) and its Fourier transform X(jω) are said to form a Fourier transform pair denoted as
Existence of Fourier Transform
A function x(t) has a unique Fourier transform if the following conditions are satisfied, which are also referred to as Dirichlet Conditions:
Dirichlet Conditions:
(i) It must be absolutely integrable That is,
(ii) x(t) has a finite number of maxima and minima and a finite number of discontinuities within any finite interval.
The above conditions are only sufficient conditions, but not necessary for the signal to be Fourier transformable. For example, the signals u(t),r(t) and cos(ω0t) are not absolutely integrable but still possess a Fourier transform.
Magnitude and Phase Spectrum
The Fourier transform X(jω) of a signal x(t) is in general, a complex form that can be expressed as
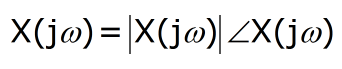
The plot of |X(jω)| versus ω is called the magnitude spectrum of x(t) and the plot of ∠jω versus ω is called the phase spectrum. The amplitude (magnitude) and phase spectra are together called Fourier spectrum which is nothing but the frequency response of X(jω) for the frequency range – infinity to + infinity.
Inverse Fourier Transform
The inverse Fourier transform of X(jω) is given as
This method of calculating the inverse Fourier transform seems difficult as is involves integration. There is another method to obtain inverse Fourier transform using partial fraction. Let a rational Fourier transform is given as
X(jω) can be expressed as a ratio of two factorized polynomials in jω as shown below.
By the partial fraction expansion technique, the above can be expressed as shown below.
where k1,k2 ……kn calculated depending on whether the roots are real and simple or repeated or complex.
Properties of Fourier Transform
There are some properties of continuous time Fourier transform (CTFT) based on the transformation of signals, which are listed below.
a. Linearity:
The linearity property states that, the linear combination of signals in the time domain is equivalent to a linear combination of their Fourier transform in the frequency domain.
where a and b are any arbitrary constants.
b. Time Shifting:
The time-shifting property states that the delay of t0 in the time domain is equivalent to the multiplication of e-jωto with its Fourier transform. It implies that the amplitude spectrum of the original signal does not change but the phase spectrum is modified by a factor of -jωt0.
c. Conjugation and Conjugate Symmetry:
d. Time Scaling
The time scaling property states that the time compression of a signal in the time domain is equivalent to expansion in the Frequency domain and vice-versa,
e. Differentiation in Time-Domain
The time differentiation property states that differentiation in the time domain is equivalent to multiplication of jω in the frequency domain.
f. Integration in Time-Domain:
g. Differentiation in Frequency Domain:
The differentiation of the Fourier transform in the frequency domain is equivalent to the multiplication of the time domain signal with -jt .
Differentiation in Frequency Domain
h. Frequency Shifting:
The frequency-shifting property states that a shift of ω0 in frequency is equivalent to multiplying the time domain signal by ejωto
i. Duality Property:
j. Time Convolution:
Convolution between two signals in the time domain is equivalent to the multiplication of Fourier transforms of the two signals in the frequency domain.
k. Frequency Convolution:
Convolution in the frequency domain (with a normalization factor of 2π) is equivalent to the multiplication of the signals in the time domain.
l. Area Under x(t):
If X(jω) is the Fourier transform of x(t), then,
that is, the area under a time function x(t) is equal to the value of its Fourier transform evaluated at ω= 0
5.m. Area Under X(jω):
If X(jω) is the Fourier transform of x(t), then,
n. Parseval’s Energy Theorem:
If X(jω) is the Fourier transform of an energy signal x(t). then
where Ex is the total energy of the signal x(t).
Get complete information about the GATE exam pattern, cut-off, and all those related things on the BYJU’S Exam Prep official youtube channel.



