- Home/
- GATE ELECTRICAL/
- GATE EE/
- Article
Nyquist Stability Criteria & Analysis Study notes For EE/EC
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Nyquist stability criteria and analysis are essential tools in control systems engineering for assessing the stability of a closed-loop control system using frequency domain methods. It is an extension of the Bode stability criterion and is based on the Nyquist plot.
In this article, you will find the study notes on Nyquist stability Criteria & Analysis which will cover the topics such as the Nyquist Stability principle, the Cauchy Principle, the Concept of Encirclement & Enclosement, Nyquist Plot, Phase Margin & Gain Margin with the help of Nyquist Plot. These study notes are sure to help you prepare for engineering related exams like GATE, ISRO, ESE, and others.
Download GATE Electrical Engineering Revision Sheet and Formulae PDF
Table of content
Polar Plot
The polar plot of a sinusoidal transfer function G(jω) is a plot of the magnitude of G(jω) versus the phase angle of G(jω) on polar coordinates as ω varied from zero to infinity.
Step 1: Determine Transfer Function G(jω)
- Start with the transfer function of the system, which represents the ratio of the output to the input in the Laplace domain.
Step 2: Evaluate G(jω) at Various Frequencies
- For different values of ω (angular frequency), evaluate G(jω) to obtain complex-valued results.
Step 3: Separate Magnitude and Phase
- From the complex-valued results, extract the magnitude |G(jω)| and phase angle φ of G(jω).
Step 4: Convert Magnitude to Decibels (Optional)
- If the magnitude is given in linear units, you may convert it to decibels using the formula: Magnitude (dB) = 20 * log10(|G(jω)|).
Step 5: Plotting the Polar Plot
- Use a polar coordinate system to plot the frequency values along the angular direction (usually the x-axis) and the magnitude or phase values along the radial direction (y-axis).
- For magnitude, plot the magnitude values at their corresponding angles.
- For phase, plot the phase values at their corresponding angles.
Step 6: Connect the Points (Optional)
- To obtain a smoother curve, you can connect the points on the polar plot using a smooth line or spline.
Step 7: Interpret the Polar Plot
- Analyze the polar plot to gain insights into the system’s frequency response. Look for frequency regions with large or small magnitude values, as well as regions of phase shift.
Step 8: Adjust the Plot (Optional)
- If necessary, you can adjust the frequency range or parameters of the system to see how it affects the polar plot.
It’s important to note that the polar plot is a representation of the frequency response of the system in the complex plane. The magnitude and phase information is essential for understanding the system’s stability, frequency-domain behaviour, and other characteristics. Polar plots are often used to analyze and design systems with frequency-dependent responses, such as filters and control systems.
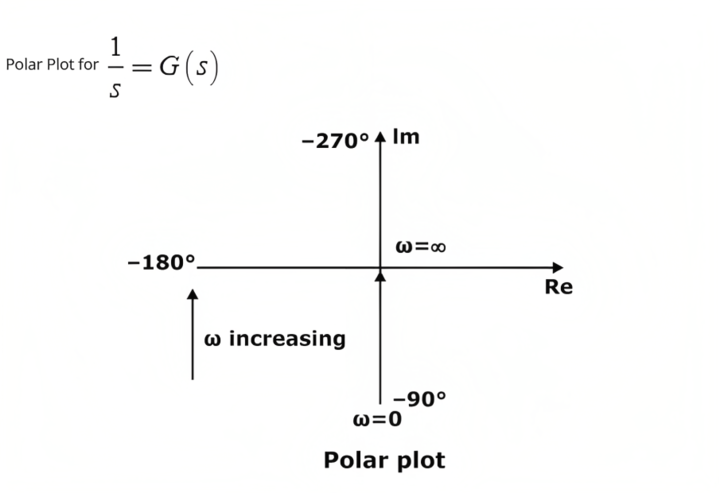
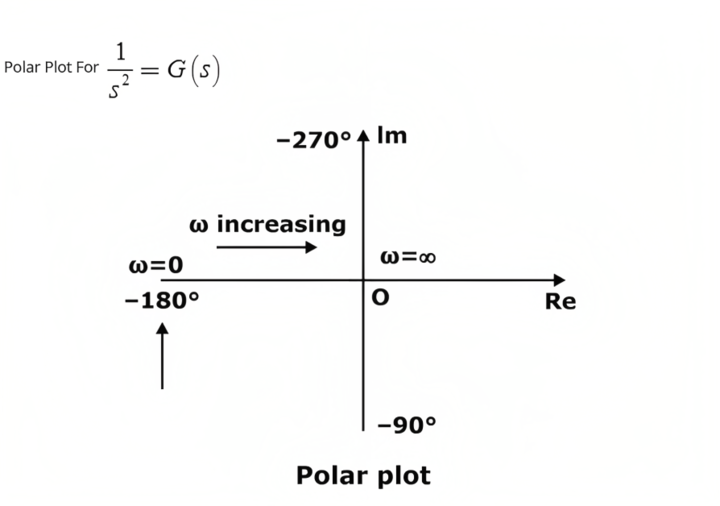
Polar Plot of Some Standard Functions
- Type 0 System ;

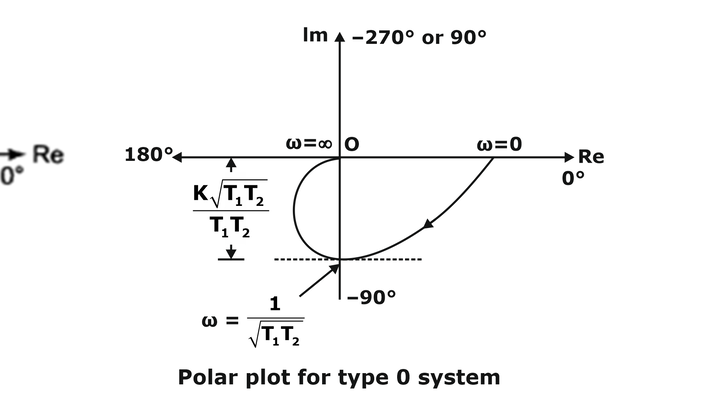
- Type 1 System
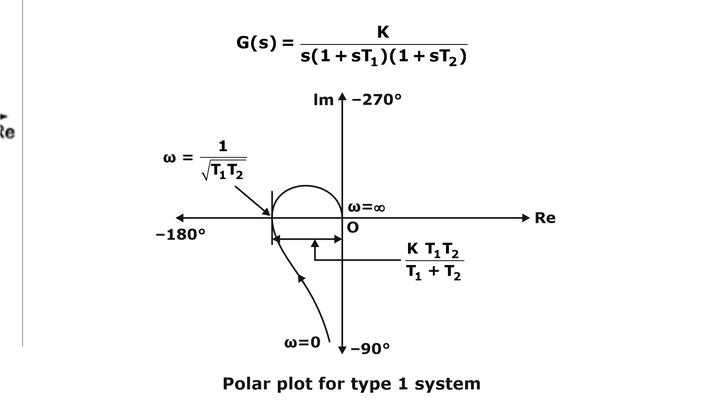
- Type 2 System

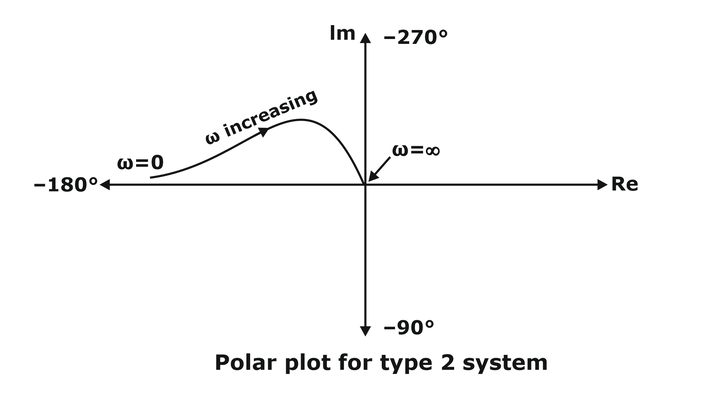
Introduction of Additional Pole

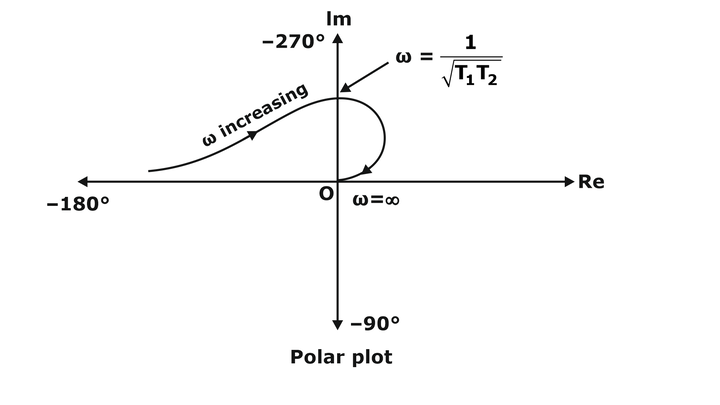
Gain Margin and Phase Margin with Polar Plot
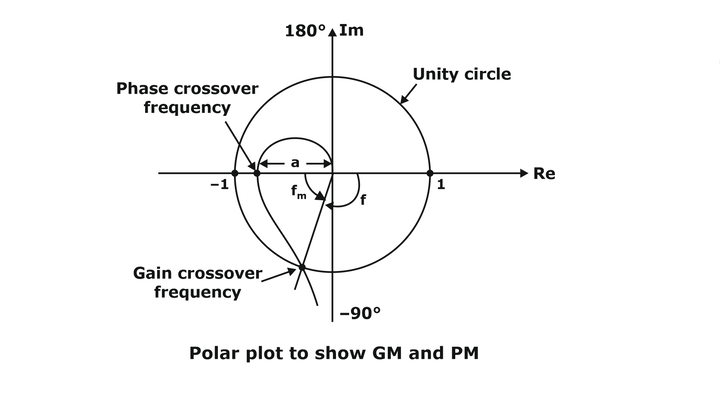
- Phase Crossover Frequency: The frequency at which the polar plot crosses the -180° line is called phase crossover frequency.
- Gain Crossover Frequency: The frequency at which the polar plot crosses the unity circle is called gain crossover frequency.
- Gain Margin: At phase crossover frequency, if the gain is ‘a’ then
Gain margin = – 20 log a
- Phase Margin (φm): At gain crossover frequency, if the phase is φ then the phase margin
φm = 180 + φ
where φ is positive from the anti-clockwise direction.
Download Formulas for GATE Electrical Engineering – Signals and Systems PDF
Nyquist Stability Criterion
A stability test for time-invariant linear systems can also be derived in the frequency domain. It is known as the Nyquist stability criterion. It is based on the complex analysis result known as Cauchy’s principle of argument. Nyquist criterion is used to identify the presence of roots of a characteristic equation of a control system in a specified region of the s-plane. The Nyquist approach is the same as Routh-Hurwitz but, but it differs in the following aspect
- The open loop transfer function G(s)H(s) is considered instead of the closed loop characteristic equation 1+G(s) H(s) = 0.
- Inspection of the graphical plot of G(s) H(s) enables us to get more than a yes or no answer to the Routh-Hurwitz method pertaining to the stability of the control system.
- Nyquist plots display both amplitude and phase angle on a single plot, using frequency as a parameter in the plot.
- Nyquist plots have properties that allow you to see whether a system is stable or unstable. It will take some mathematical development to see that, but it’s the most useful property of Nyquist plots.
Concept of Encirclement;& Enclosement
Encirclement:
- point A is encircled in the counter in Counter Clock Wise by a closed path, while point B is NOT encircled by the closed path.
Enclosement: A point or region is said to be enclosed by a closed path if the point or region lies to the right of the path when the path is traversed in any prescribed direction.
- In Figure (a) point A is not enclosed by Path, while Point B is enclosed by a path.
- In Figure (b); point A is enclosed by Path, while point B is not enclosed by the path.
Download Formulas for GATE Electrical Engineering – Electrical Machines PDF
Nyquist Stability Criterion: Fundamentals
Consider the phasor from point A to S1;of encirclement = N, the net angle traversed by the phasor = 2πN rad
- In figure (a) Point A of encirclement = +1; Point B of encirclement = +2.
- In figure (b) Point A of encirclement = -1; Point B of encirclement = -2.
Determination of N:
- For a SISO feedback system the closed-loop transfer function is given by
- closed-loop system poles are obtained by solving the following equation
1+G(s)H(s) =0 =Δ(s) ;represents the system characteristic equation.
- In the following, we consider the complex function
D(s) = 1+G(s)H(s)
- The zeros of D(s) are the closed-loop poles of the transfer function. Here now we concluded that the poles of D(s) are the zeros of M(s).
- At the same time the poles of D(s) ; are the open-loop control system poles since they are contributed by the poles of H(s)G(s), which can be considered as the open-loop control system transfer function—obtained when the feedback loop is open at some point.
- The Nyquist stability test is obtained by applying the Cauchy principle of argument to the complex function D(s). First, we state Cauchy’s principle of argument.
Cauchy’s Principle of Argument
- Let F(s) be an analytic function in a closed region of the complex s-plane, except at a finite number of points (namely, the poles of F(s)).
- It is also assumed that F(s) is analytic at every point on the contour. Then, as ‘s’ travels around the contour in the s-plane in the clockwise direction, the function F(s) ; encircles the origin in the [ReF{(s)}, Img{F(s)}]-plane in the same direction N times, where N given By
N= P-Z
where Z and P stand for the number of zeros and poles (including their multiplicities) of the function F(s) inside the contour.
- The above result can be also written as ;
arg{F(s)} = (Z-P)2π = 2Nπ
Nyquist Plot
The Nyquist plot is a polar plot of the function D(s) = 1+ G(s)H(s) when travels around the contour
- The contour in the above figure covers the whole unstable half plane of the complex plane s, R→∞.
- Since the function D(s), according to Cauchy’s principle of argument, must be analytic at every point on the; contour, the poles D(s) of the imaginary axis must be encircled by
infinitesimally small semicircles.
Nyquist Criterion:
- It states that the number of unstable closed-loop poles is equal to the number of unstable open-loop poles plus the number of encirclements of the origin of the Nyquist plot of the complex function F(s).
- The above criterion can be slightly simplified if instead of plotting the function D(s) = 1+G(s)H(s), we plot only the function G(s)H(s); and count encirclement of the Nyquist plot of G(s)H(s); around the point (-1+j0). ;
- The number of unstable closed-loop poles (Z) is equal to the number of unstable open-loop poles (P) plus the number of encirclements (N) of the point (-1+j0) ; of the Nyquist plot of G(s)H(s), that is
Z= P+N
Phase and Gain Stability Margins
Two important notions can be derived from the Nyquist diagram: phase and gain stability margins. The phase and gain stability margins are presented in the Figure below
- They give the degree of relative stability; in other words, they tell how far the given system is from the instability region. Their formal definitions are given by
- where ωgc and ωpc ; stand for, respectively, the gain and phase crossover frequencies, which are obtained from the figure as ;
Example: ; Consider a control system represented by
Solution: Since this system has a pole at the origin, the contour in the -plane should encircle it with a semicircle of an infinitesimally small radius. This contour has three parts (a), (b), and (c). Mappings for each of them are considered below.
- On this semicircle the complex variable ‘s’; is represented in the polar form by ‘s = Rejψ‘ ; with R→∞, – π/2 ≤;ψ ;≥;π/2. Substituting ‘s = Rejψ‘; into G(s)H(s), we easily see that G(s)H(s)→0; Thus, the huge semicircle from the -plane maps into the origin in the -plane.
Thus, the huge semicircle from the s-plane maps into the origin in the G(s)H(s)-plane.
- On this semicircle the complex variable is represented in the polar form by ‘s = rejψ‘ ;with r→0, – π/2 ≤ ψ ;≥ ;π/2. so that we have
Since φ ;changes from ‘– π/2‘ at point A to ‘ ;π/2‘ at point B, ;arg{G(s)H(s)} ;will change from π/2 ;to –π/2 . We conclude that the infinitesimally small semicircle at the origin in the s-plane is mapped into a semicircle of infinite radius in the G(s)H(s)-plane.
- On this part of the contour s; takes pure imaginary values, i.e. s= jω; with ω changing from’-∞ ; to +∞’.Due to symmetry, it is sufficient to study only mapping along 0+≤ ω ≥+∞. We can find the real and imaginary parts of the function G(jω)H(jω), which are given by
From the above expressions, we see that neither the real nor the imaginary parts can be made zero, and hence the Nyquist plot has no points of intersection with the coordinate axis. For ω= 0+ we are at point B and since the plot at ω=;+∞ ; will end up at the origin. Note that the vertical asymptote of the Nyquist plot is given by
{Re G(jo±)H(jo±)} = -1
- From the Nyquist diagram, we see that N= 0 ; and since there are no open-loop poles in the left half of the complex plane, i.e…P=0, we have Z =0; so that the corresponding closed-loop system has no unstable poles.
If you are preparing for GATE and ESE, avail Online Classroom Program to get unlimited access to all the live structured courses and mock tests from the following link:



