Study notes on Symmetrical Component & Symmetrical Fault Analysis: Electrical Engineering

Symmetrical Components

A three-phase system is said to be symmetrical when the system viewed from any phase is similar. Thus, in a three-phase symmetrical system the self-impedance of all the three phases are equal and the mutual impedances, if any between the three phases are the same any three phase system having unbalanced phasor quantities can be represented in terms of three phase balanced phasor components as a combination of positive, negative and zero sequence component, which are as follows:

V_a = V_ao + V_a1+ V_a2

Vb = V_bo + V_b1+ V_b2

Vc = Vc_o + V_c1+ V_c2

Also Read: Component of Power System For Electrical Engineering

Positive Phase Sequence Components

It represents a set of balance phasors V_a1, V_b1 & V_c1 These components have three phasors equal in magnitude displaced by 120^o and having same phase sequence as original phasors.

Negative Phase Sequence Components

These components have three phasors V_a2, V_b2 & V_c2 equal in magnitude displaced by 120^o but having phase sequence opposite to original phasors. It represents a set of balanced phasors

Download Formulas for GATE Electrical Engineering – Signals and Systems PDF

Zero Sequence Components

These phasors V_ao, V_bo & V_co are equal in magnitude and having zero phase displacement.

α operator = e^+j120° = – 0.5 + j 0.866

α² = e^+j240° = – 0.5 – j 0.866

α³ = 1

α⁴ =α

1 + α + α² = 0

In matrix form

Three Phase Power in Terms of Symmetrical Components

= sum of symmetrical components power

Sequence Impedance

The positive sequence impedance of an equipment is the impedance offered by the equipment to the flow of positive sequence current. similarly, the negative sequence or zero sequence impedance of the equipment is the impedance offered by the equipment to the flow of corresponding sequence current.

Sequence Impedance of a Transmission Line

Positive sequence impedance Z₁ = Z_s – Z_m

Negative sequence impedance Z₂ = Z_s – Z_m

Zero sequence impedance Z₀ = Z_s + 2Z_m

where, Z_s = Self-impedance per phase

Z_m = Mutual impedances between phases

Sequence Impedance of Synchronous Machine

1. Positive Sequence, Impedance Z₁ Depending on the time interval of interest one of the three reactance may be used.
   • For the sub transient interval, we use sub transient reactance Z”₁ = j X”_d
   • For the transient interval, we use the transient reactance Z’₁ = j X’_d
   • If the steady state value is of interest we have Z₁ = j X_d
2. Negative Sequence Impedance
   

3. Zero Sequence Impedance (Z₀) Zero sequence current are all in phase and therefore, do not reproduce any rotating field. The zero sequence impedance Z₀ depends upon the type of grounding and the zero sequence impedance per phase of the generator.

Sequence Networks Equations

Sequence Network of Unloaded Alternator

1. Positive Sequence Network

2. Negative Sequence Network

3.Zero Sequence Network

Download Formulas for GATE Electrical Engineering – Electrical Machines PDF

Sequence Impedance of Transformers

• Switch A is closed when primary winding is star connected with neutral grounded.
• Switch C is closed when primary winding is delta connected.
• Switch B is closed when secondary winding is star connected with neutral grounded.
• Switch D is closed when secondary winding is delta (∆) connected.

• Keep both A and C open if when primary winding is star connected with natural isolated (not grounded).
• Keep both B and D open if when secondary winding is star connected with natural isolated.

where Z₀ = Zero sequence impedance of transformer.

Examples

Fault may occur at different points in power system.

Faults that occur on a power system are broadly classified as follows

Transient on a Transmission Line

When a sudden change in voltage and current distribution takes place, a power energy distribution also changes. But energy distribution is called transient phenomenon in power system.

The current after short circuit I(t) has components i.e.,

I = I_s + I_t

Where, I_s = Steady state value of current

I_t = Transient current

3-ϕ Sudden Short Circuit of an Unloaded Alternator

Whenever a three-phase short circuit occurs at the terminals of an alternator, the armature current suddenly increases to a large value and voltage across its terminals drops.

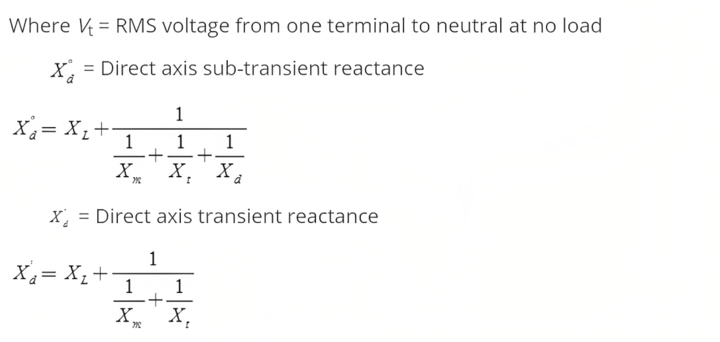
X_d = Direct axis synchronous reactance

X_d = X_L + X_m

Where X_L = Leakage reactance

X_m = Main winding reactance

X_t = Field winding reactance

X_d = Damper winding reactance

Note:

Symmetrical Fault Analysis

Three Phase Fault

Symmetrical short circuit on Synchronous Machine The selection of a circuit breaker for a power system depends not only upon the current the breaker is to carry under normal operating conditions but also upon the maximum current it may have to carry momentarily and the current it may have to interrupt at the voltage of the line in which it is placed.

In order to approach the problem of calculating the initial current, we need to study the behavior of a synchronous generator when it is short-circuited. When an ac voltage is applied suddenly across a series R-L circuit, the current which flows has two components 1.

a steady state sinusoidal varying component of constant amplitude and 2. a non-periodic and exponentially decaying with a time constant of L/R. (which is also referred as the dc component current).The initial value of the dc component of current depends on the magnitude of the ac voltage when the circuit is closed.

In such types of faults, all the three phases are short-circuited to each other and often to earth also. Such faults are balanced and symmetrical in the sense that the system remains balanced even after the fault.

Fault Level Calculations
In a power system, the maximum fault current (or fault MVA) that can flow into a zero impedance fault is necessary to be known for switchgear solution. This can either be the balanced three phase value or the value at an asymmetrical condition.

The Fault Level defines the value for the symmetrical condition. The fault level is usually expressed in MVA (or corresponding per-unit value), with the maximum fault current value being converted using the nominal voltage rating.

The Short circuit capacity (SCC) of a busbar is the fault level of the busbar. The strength of a busbar (or the ability to maintain its voltage) is directly proportional to its SCC. An infinitely strong bus (or Infinite bus bar) has an infinite SCC, with a zero equivalent impedance and will maintain its voltage under all conditions.

Key Points

• Positive sequence currents are present in all types of faults.
• Negative sequence currents are present in all unsymmetrical faults.
• Zero sequence currents are present when the natural of the system is grounded and the fault also involves the ground and the magnitude of the natural current (I_n) is equal to 3I_ao.
• Voltage of natural V_n = -I_nZ_n = -3I_aoZ_n
• Shunt faults are characterized by increase in current and fall in voltage and frequency whereas series faults are characterized by increase in voltage and frequency and fall in current in the faulted phases.

Download Formulas for GATE Electrical Engineering – Signals and Systems

If you are preparing for GATE and ESE, avail Online Classroom Program to get unlimited access to all the live structured courses and mock tests from the following link:

Online Classroom Program

BYJU’S Exam Prep Test Series