Combinational Circuits (Part 2) Study Notes for GATE Exams

Designing Combinational Circuits

The following steps, to design combinational circuits are:

• Understand the problem
• Find the required number of input-output variables
• Construct the truth table using the relationship between the input and output
• Obtain either the Boolean function or the logical expression from the truth table using Karnaugh Map.
• Draw the logic circuit based on the obtained logical expression.

Arithmetic Circuits

Arithmetic circuits are used to perform addition and subtraction. Binary adder performs binary addition while binary subtractor performs binary subtraction.

Classification of Adder:

• Half Adder
• Full Adder

Classification of Subtractor: 

• Half Subtractor
• Full Subtractor

Half Adder:

This circuit is used for the addition of 2 one-bit numbers.

The truth table of Half Adder:

• Half adder circuit:

        Sum (S) = 

        Carry (C) = AB

• Implement of Half Adder Using NAND Gate:

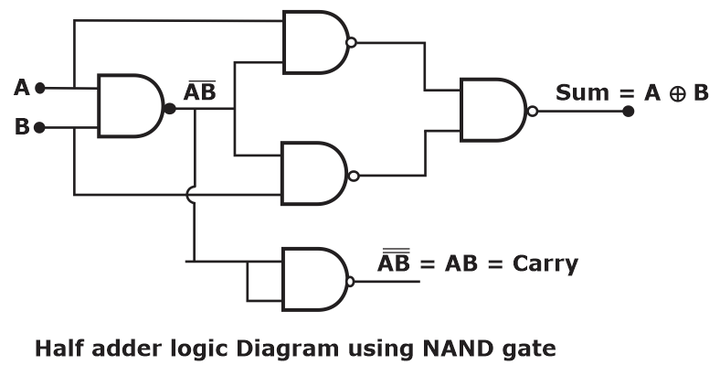
Note: Required number of NAND Gates to implement the Half Adder = 5

• Implement of Half Adder Using NOR Gate:

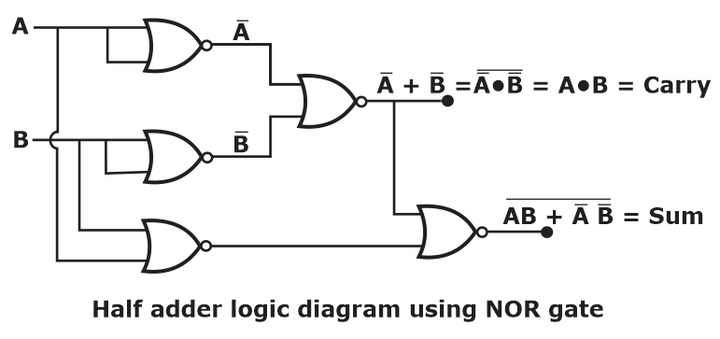
Note: Required number of NOR Gates to implement the Half Adder = 5

Full Adder:

A full adder is a combinational logic circuit that performs the arithmetic sum of three input bits. It consists of three inputs and two outputs.

• The truth table for Full Adder:

•  The logic diagram of Full Adder:

Sum (S) = 

Carry (C0) = AB + BC + AC

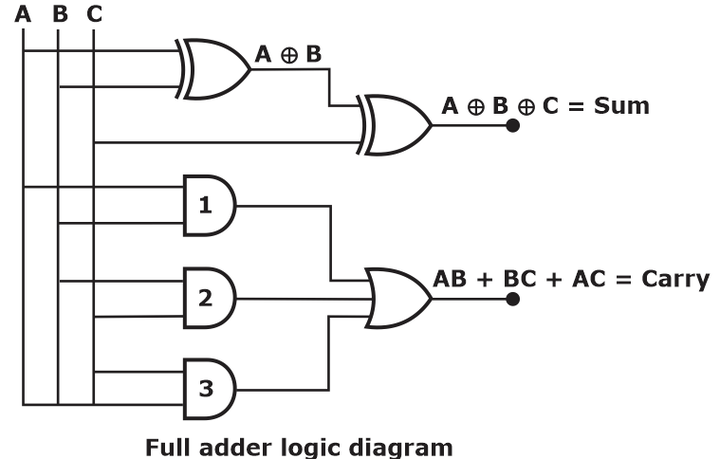
• A full adder made from 2 Half adder + 1 OR Gate
• Required minimum number of NAND gates to implement Full Adder = 9
• Required minimum number of NOR gate to implement Full Adder = 9

Half Subtractor:

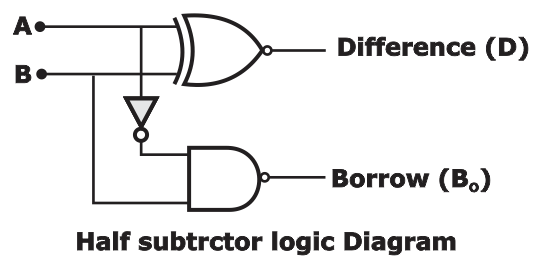
• Logic Diagram of Half Subtractor:

• To implement half subtractor the total number of NAND/NOR are required = 5

Full Subtractor:

It is a combinational logic circuit that performs subtraction involving three-bit namely minuend bit, subtrahend bit and borrows from the previous stage

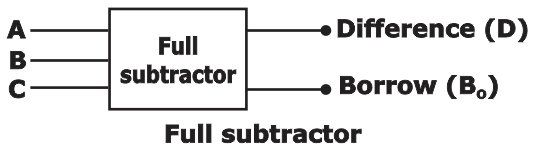
• Difference (D) 
• 
  • A full subtractor = 2 half subtractor + 1 OR gate
  • To implement full subtractor from NAND or NOR gates required = 9 gates 

Multiplexer (MUX)

• It is a combinational circuit that chooses binary information from one of the many input lines and directs it to a single output line.
• The selection of a particular input line is controlled by a set of selection lines in the circuit.
• MUX is also called: Many to one, Data selector, Universal circuit, or Parallel data serial.
• Multiplexing means transmitting a large number of information units over a small number of channels or lines. It is abbreviated as MUX.
• There are 2n input lines and ‘n’ selection lines whose bit combinations determine which input is selected.
• m = 2n implies n = log m where m = Number of data inputs, and n = Number of select lines

2 × 1 MUX :

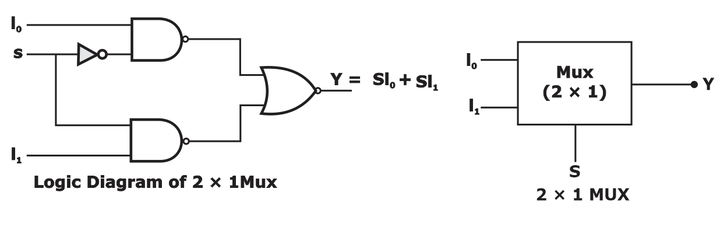
• Implementation of one MUX using another MUX:

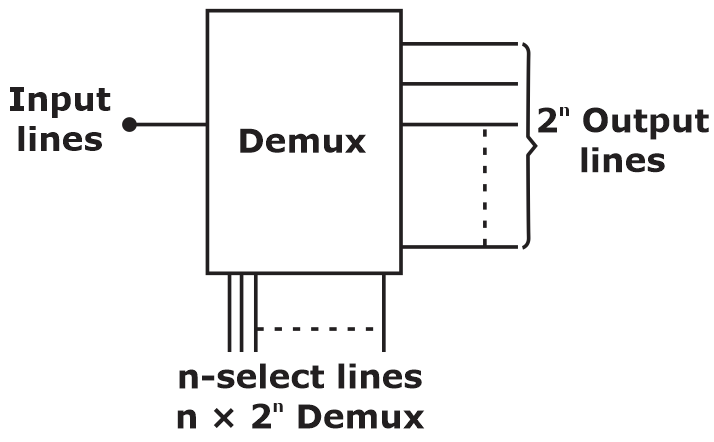
Demultiplexer (DEMUX)

• It is a circuit that receives information on a single line and transmits this information on one of 2n possible output lines.
• The selection of a specific output line is controlled by the bit values of n selected lines.

1 × 2 Demux:

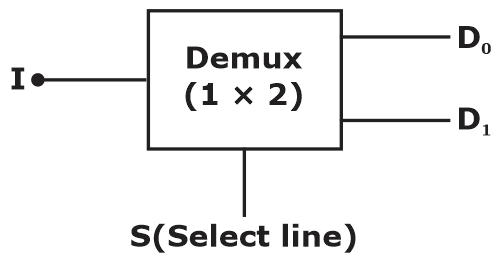
D0 = S′I

D1 = SI

• The truth table of 1 × 2 Demux:

1 × 4 Demux:

• The Truth table of 1 × 4 Demux:

• Circuit Diagram of 1 × 4 Demux:

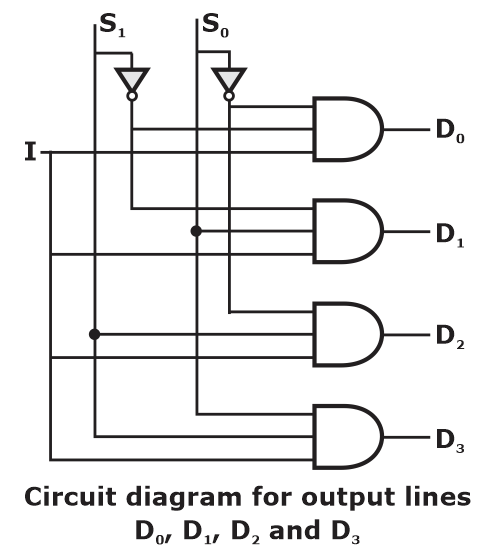
• DEMUX Implementation using another DEMUX:

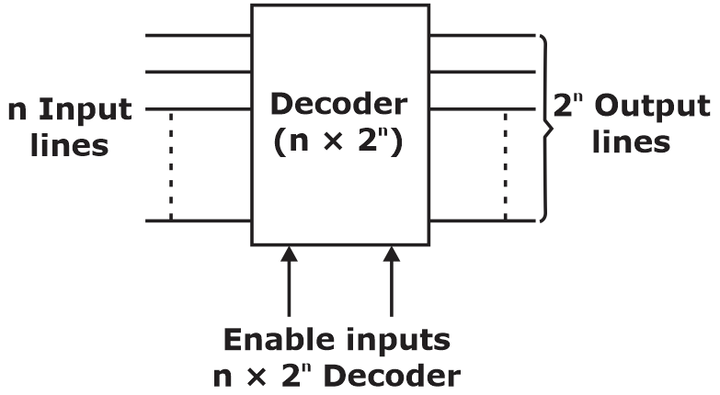
Decoders

• A decoder is a combinational type circuit that converts binary information from n input lines to maximum 2n unique output lines.
• If the n-bit decoded information has unused or doesn’t care about combinations, the decoder output will have fewer than 2n outputs.
• The decoders explained here are n-to-m-line decoders, where m ≤ 2n. Their purpose is to generate the 2n (or fewer) minterms of n input variables.

2 × 4 Decoder:

The Truth table of 2 × 4 Decoder:

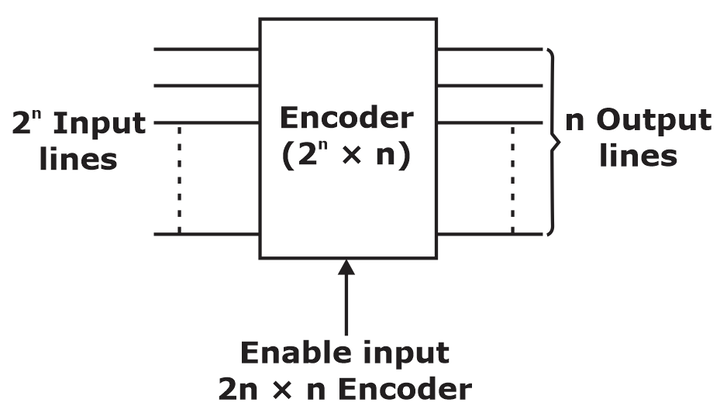
Encoders

• It is a combinational circuit that converts information into the coded form (binary).
• It is a digital circuit that performs the inverted operation of a decoder circuit.
• An encoder has 2n (or fewer) input lines and n output lines.
• The output lines generate the binary code corresponding to the input value in the circuit.

If you are preparing for GATE and ESE, avail of an online classroom program to get unlimited access to all the live structured courses and mock tests from the following link :

ESE and GATE ECE Online Classroom Program (24+ Live classes and 150+ mock tests)

ESE and GATE EE Online Classroom Program (24+ Live classes and 193+ mock tests)

Daily free APP and Youtube classes, Engineering Jobs, Free PDF & much more, Join our Telegram Group Join Now.