The maximum number of linearly independent rows in a matrix A is called the row rank of A, and the maximum number of linearly independent columns in A is called the column rank of A. If A is an m by n matrix, that is, if A has m rows and n columns, then it is obvious that

Example 1: Find the rank of the matrix

First, because the matrix is 4 x 3, its rank can be no greater than 3. Therefore, at least one of the four rows will become a row of zeros. Perform the following row operations:

Since there are 3 nonzero rows remaining in this echelon form of B,  

3. Eigenvalues and Eigenvectors

A = [a_ij] be a square matrix of order n.  if there exists a non-zero column vector X and a scalar l such that AX = lX, then l is called Eigen value of the matrix A and X is called an Eigen vector corresponding to the eigen value l.

Characteristic Matrix:

            The matrix |A – I| is called characteristic matrix of given matrix A which is obtained by subtracting l from diagonal elements of A.

Characteristic Polynomial:

            The determinant |A – I| when expanded will give a polynomial of degree n in l which is called characteristic polynomial of matrix A.

Characteristic equation:

            The equation |A - II| = 0 is called characteristic equation or secular equation of matrix A.

Characteristic Roots or Eigenvalues or Latent roots:

            The roots of the characteristic eq.  l₁, l₂ ……… l_n are called characteristic roots or Eigenvalues or Latent roots.

Characteristic Vectors or Eigen Vectors:

            Corresponding to each characteristic root l there corresponds non-zero vector X satisfying the equation (A - I). X = 0.  The non-zero vectors X are called characteristic vectors or Eigen vectors.

Spectrum of a Matrix:

            The set of all Eigenvalues of given matrix A is called the spectrum of A

Example: Find Eigenvalues and Eigenvectors of a 2x2 Matrix

If

then the characteristic equation is 

and the two eigenvalues are

λ₁=-1, λ₂=-2

All that's left is to find the two eigenvectors.  Let's find the eigenvector, v₁, associated with the eigenvalue, λ₁=-1, first.

so clearly from the top row of the equations, we get

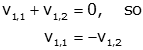
Note that if we took the second row we would get

In either case we find that the first eigenvector is any 2 element column vector in which the two elements have equal magnitude and opposite sign.

where k₁ is an arbitrary constant.  Note that we didn't have to use +1 and -1, we could have used any two quantities of equal magnitude and opposite sign.

Going through the same procedure for the second eigenvalue:

 Again, the choice of +1 and -2 for the eigenvector was arbitrary;

 Thanks,

Team Gradeup!