Columns and Struts:
- A structural member subjected to an axial compressive fore is called strut. As per definition strut may be horizontal, inclined or even vertical.
- Vertical strut is called a column.
Euler’s Column Theory: This theory has the following assumptions.
- Perfectly straight column and axial load apply.
- Uniform cross-section of the column throughout its length.
- Perfectly elastic, homogeneous and isotropic material.
- Length of column is large as compared to its cross-sectional dimensions.
- The shortening of column due to direct compression is neglected.
- The failure of column occurs due to buckling alone.
Limitation of Euler’s Formula
- There is always crookedness in the column and the load may not be exactly axial.
- This formula does not take into account the axial stress and the buckling load given by this formula may be much more than the actual buckling load.
Euler’s Buckling (or crippling load): The maximum load at which the column tends to have lateral displacement or tends to buckle is known as buckling or crippling load. Load columns can be analysed with the Euler’s column formulas can be given as


where, E = Modulus of elasticity, l = Effective Length of column, and I = Moment of inertia of column section.
- For both end hinged:
n=1


- For one end fixed and other free:


- For both end fixed:
n=2,


- For one end fixed and other hinged:


Effective Length for different End conditions:
Modes of failure of Columns
Slenderness Ratio ( λ) Slenderness ratio of a compression member is defined as the ratio of its effective length to least radius of gyration.
Buckling Stress:
Rankine’s Formula for Columns: It is an empirical formula, takes into both crushing PCS and Euler critical load (PR).

PR = Crippling load by Rankine’s formula
Pcs = σcs A = Ultimate crushing load for column
 Crippling load obtained by Euler’s formula
Crippling load obtained by Euler’s formula

Where, A = Cross-section are of column, K = Least radius of gyration, and A = Rankine’s constant.
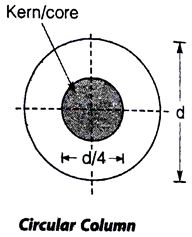
Shape of kern in eccentric loading:
- To prevent any kid of stress reversal, force applied should be within an area near the cross section called as CORE or KERN.
- Shape of kern for rectangular and l-section is Rhombus and for square section shape is square for circular section shape is circular.


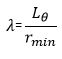







Comments
write a comment