Set Theory & Venn Diagram Formulas and Concepts
By BYJU'S Exam Prep
Updated on: September 13th, 2023

Dear Aspirants,
In this article, we will learn about various concepts related to the Set Theory & Venn Diagram. Set Theory & Venn Diagram are some of the most common topics tested in the CAT exam. This is an important topic for Data Interpretation & Logical Reasoning section in CAT.
![]()
Table of content
Dear Aspirants,
In this article, we will learn about various concepts related to the Set Theory & Venn Diagram. Set Theory & Venn Diagram are some of the most common topics tested in the CAT exam. This is an important topic for Data Interpretation & Logical Reasoning section in CAT.
![]()
A set is a well-defined collection of objects. We can have: {1,2,3,4,5,…} set of natural numbers N, or {0,1,2,3,4,…} set of whole numbers W, or {0, ±1, ±2, ±3, ±4, …} set of integers, etc
n(A) denotes the number of elements in set A.
Hence, if A = {set of positive odd numbers up to 10}, then n(A) = 5.
Universal Set:
It is the set containing all the elements under consideration.
Eg: If we are talking about the English alphabet, then the elements A, B, C, D, …, Z are in the universal set, say U. Then if we talk of vowels only V = (A, E, I, O, U),
We find that all the elements of V are also elements of the universal set. V is called the subset of U.
Compliment
A set containing all the elements belonging to the universal set but not to a particular set. Thus complement of V would be the set containing all the consonants, denoted by V’.
Union
If A and B are set, then A∪B denoted union, which means all the elements which are either in A or in B or both A and B.
Intersection
Denoted by A∩B, consist of all elements which are in both A and B.
If A and B have no elements in common, they are called disjoint or non-overlapping sets.
VENN DIAGRAMS
We can represent sets by way of diagrams.
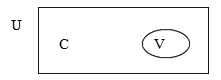
In this diagram, the Universal set (U) is the set of alphabets of English, and the vowels will be a subset of this. All other elements represent the consonants.
Rules:
(1) n(A∪B) = n(A) + n(B) [if the sets are disjoint]
(2) n(A∪B) = n(A) + n(B) – n(A∩B)
(3) If there are three sets: n(A∪B∪C) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C).
Venn Diagrams of 2 sets
If the two given objects are called ‘A’ & ‘B’. The sum of ‘A’ & ‘B’ here is known as “A union B” and is symbolically represented as “A ∪ B”.
A ∪ B = A + B – A ∩B.
A ∩ B is called “An intersection B”; or that part which is common in A & B.
A ∩ B is subtracted once from the sum of A & B because it is included twice in the total, being A part of both A & B.
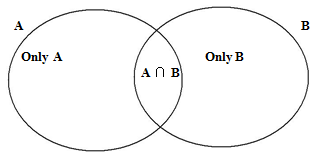
If the value of ‘A union B’ is to be calculated from the diagram, the sum of these 3 values given inside the diagram will give A∪B. Because one part represents only ‘A’, the other part only ‘B’, and the third common part A∩B.
Illustration 1: In the locality, 2500 persons read Times of India and 3500 persons read The Hindustan Times. 250 persons read both of these newspapers. Find the number of persons who read 1 or 2 of these newspapers.
Solution: We have to find A∪B in this case hence 2500 + 3500 – 250 = 5750.
Illustration 2: In a class, 120 students play Hockey, 145 students play Cricket. 10 students play both of these games. The total number of students in the class is 280. Find:
1. The no. of students playing 1 or more games.
2. The no. of students playing no game.
3. The no. of students playing only Cricket.
4. The no. of students playing only Hockey.
Solution: Refer to the diagram

1. Students who play one or more of these two games = H∪C → 110 + 10 + 135 = 255.
2. Total no of students in the class are given to be 280, as only 255 play one or more games, this implies the remaining students play none of these games i.e. 280 – 255 = 25.
3. From the diagram that 135 students play only Cricket.
4. From the diagram that 110 students play only Hockey.
VENN DIAGRAM OF THREE SETS
In three sets ‘A’, ‘B’ & ‘C’,
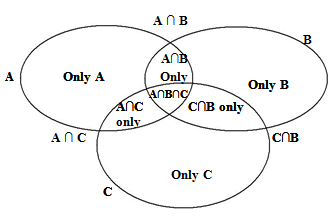
Illustration 3: A survey was conducted on a sample of 1000 persons concerning their knowledge of English, French, and German. The results of the survey are presented in the diagram below. The ratio of the number of persons who do not know any of the three languages to those who know all the three languages is:

- 1/27 2. 1/125 3. 7/175 4. 175/1000
Solution: Count the number in the diagram: 993. Hence we get that 7 do not know any language. From the diagram, we also see that 175 know all three languages. Hence 7/175.
Illustration 4. 52 students speak Hindi or English or German. There are 33 Hindi-speaking people, 37 are English speaking, and 32 are German-speaking. 22 speak Hindi and English, 20 speak German and Hindi, and 25 speak English and
German. How many speak all three languages?
- 17 2. 27 3. 37 4. none of these
Solution: We can either solve the sum by making the diagram as above, or by the formula:
N(H∪E∪G) = 52 = 33 + 37 + 32 – 22 – 25 – 20 + n(H∩E∩G), from which we get the required number as 17.
Thanks!
![]()
===========================
Download the BYJU’S Exam Prep App NOW
The most comprehensive exam prep app.
If you are aiming to crack CAT and other MBA Exam, join BYJU’S Exam Prep Online Classroom Program where you get :
- Live Courses by Top Faculty
- Daily Study Plan
- Comprehensive Study Material
- Latest Pattern Test Series
- Complete Doubt Resolution
- Regular Assessments with Report Card
#DreamStriveSucceed

