Arithmetic Progression CAT Questions – Concepts, Important Formulas, Download Sample Questions PDF
By BYJU'S Exam Prep
Updated on: September 13th, 2023

Arithmetic Progression CAT Questions are an important part of QA section of CAT. However, this section is little interesting and scoring if prepared well. Arithmetic Progression CAT Questions deal with some basic formulas, and the candidates need to prepare well to solve these questions accurately.
The candidates can expect 1-4 Arithmetic Progression CAT Questions. The difficulty level of these questions is moderate. Focusing on the basic concepts of Arithmetic Progression questions for CAT will help to understand the illustrations given in the article. BYJU’S Exam Prep experts have made a detailed analysis of Arithmetic Progression CAT to assist the candidates in their preparation.
![]()
Table of content
Arithmetic Progression CAT Questions are an important part of QA section of CAT. However, this section is little interesting and scoring if prepared well. Arithmetic Progression CAT Questions deal with some basic formulas, and the candidates need to prepare well to solve these questions accurately.
The candidates can expect 1-4 Arithmetic Progression CAT Questions. The difficulty level of these questions is moderate. You only need to focus on the basic concepts of Arithmetic Progression questions for CAT to find the illustration used in the questions. In this article, BYJU’S Exam Prep experts have made a detailed analysis of Arithmetic Progression CAT to assist the candidates in their preparation.
![]()
What are Arithmetic Progression CAT Questions?
Arithmetic progression is one of the most important topics for CAT Quant Questions. Considering the previous year’s CAT Analysis, the candidates can expect 1-4 Arithmetic Progression CAT Questions from this chapter. Arithmetic Progression or AP is a sequence of numbers in order, where the difference between any two consecutive numbers is a constant value. These are also known as Arithmetic sequences. Note the section below to get basic clearance about two concepts which you need to solve Arithmetic Progression CAT Questions.
Progression
It is not necessary that the terms of a sequence always follow a certain pattern or are described by some explicit formula for the nth term. Those sequences whose terms follow certain patterns are called progressions.
Arithmetic Progression (AP)
A sequence of numbers is said to be in Arithmetic progression if each number differs from its succeeding number by a constant value.
Common difference: Take the series: 1, 4, 7, 10, …… In this, every term increases by the same number every time. Any term deducted from the succeeding term results in the same difference of 3. (4 – 1 = 3 and 7 – 4 = 3). This is called the common difference and is denoted by ‘d’.
The AP could also have a negative common difference: 6, 3, 0, -3…..each term is reduced by 3 successively. Here the common difference is -3.
The AP can be denoted by a, a + d, a + 2d, a + 3d ……where ‘a’ is the first term and ‘d’ is a common difference.
If the number of terms in the sequence = n and its first term is a, then nth term of the AP is given by: a + (n – 1) d where d is a common difference.
The sum of n terms of an AP is given by the equation
- S = n/2 [2a + (n – 1)d]
We can also say that the Sum = (n/2)(a + L) where L is the last term of the series.
Illustration 1: Find the 20th term of series 4, 7, 10…… and also the sum of the 20 terms.
Solution:
Here a = 4, d = 3, n = 20.
20th term is given by a + (n – 1)d ⇒ 4 + 19 × 3 = 61.
Sum of 20 terms = 20/2 × [8 + 19 × 3] = 650.
Illustration 2: The sum of a certain number of terms of an A.P. is 57, and the first and last terms are 17 and 2, respectively. Find the number of terms and the common difference of the series.
Solution:
Here S = 57, a = 17, l = 2.
Using the formula S = n/2 (a + l) we get 57 = n/2 (17 + 2) ⇒ 114 = 19n, or n = 6.
Since the 6th term is 2, we can use the formula for the nth term: a + (n – 1)d ⇒ 2 = 17 + 5 × d; On solving, we get 5d = – 15 and d = -3.
Illustration 3: The ratio of the sum of n terms of two A.P. is (7n + 1) : (4n + 27). Find the ratio of their mth terms.
Solution:
Let a1, a2 be the first terms and d1, d2 the common differences between the two given A.P.
Then sums of their n terms are given by
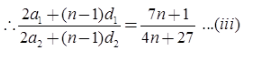
To find the ratio of the mth terms of the two given A.P.
We replace n by (2m – 1) in (iii)
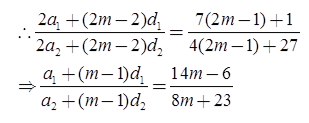
Hence the ratio of the mth terms of the two A.P. is (14m – 6) : (8m + 23).
Illustration 4: The ratio of the sums of m and n terms of an A.P. is m2: n2. Find the ratio of the mth and nth terms.
Solution: Let a be the first term and d the common difference of the given A.P. Then, the sums of m and n terms are given by Sm = m/2[2a+(m-1)d] and Sn = n/2[2a+(n-1)d], respectively. Then,
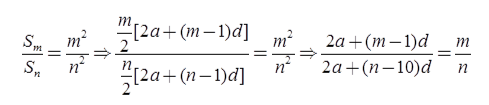
⇒ {2a+(m-1)d} n={2a+(n-1)d}m
⇒ 2a(n-m) = d {(n-1)m – (m-1)n}
⇒ 2a(n-m) = d(n-m) ⇒ d=2a
![]()
Sometimes, we require a certain number of terms in A.P. The following ways of selecting terms are generally very convenient.

In the case of an odd number of terms, the middle term is ‘a’, and the common difference is ‘d’ while in an even number of terms, the middle terms are a – d, a + d, and the common difference is 2d.
Important Properties of Arithmetic Progression
Below are some important properties of AP that you must note to solve Arithmetic Progression CAT Questions.
- If a constant is added to or subtracted from each term of an A.P., then the resulting sequence is also an A.P. with the same common difference.
- In each term of a given A.P. is multiplied or divided by a non-zero constant k, then the resulting sequence is also an A.P. with common difference kd or d/k, where d is the common difference of the given A.P.
- In a finite A.P. the sum of the terms equidistant from the beginning and end is always the same and is equal to the sum of the first and last term i.e., ak + an (k – 1) = a1 + an for all k = 1, 2, 3, …, n – 1.
- Three numbers a, b, c are in A.P. if 2b = a + c.
- A sequence is an A.P. if the sum of its first n terms is of the form An2 = Bn, where A, B are constants independent of n. In such a case, the common difference is 2A.
Illustration 5: If log10 2, log10 (2x – 1), and log10 (2x + 3) are in A.P., then find the value of x.
Solution:
log10 2, log10 (2x – 1), and log10 (2x + 3) are in A.P.
⇒ 2 log10 (2x – 1) = log10 2 + log10 (2x + 3)
⇒ log10 (2x – 1)2 = log10 2 . (2x + 3)
⇒ (2x – 1)2 = 2 . (2x + 3)
⇒ (y – 1)2 = 2 (y + 3), where y = 2x
⇒ y2 – 4y – 5 = 0
⇒ (y – 5) (y + 1) = 0
⇒ y = 5 or y = – 1
⇒ Hence 2x = 5; or x = log2 5
Insertion of Arithmetic Means
If 15, 11, 7, 3, –1 are in A.P., it follows that 11, 7, 3 are three arithmetic means between 15 and – 1.
If a, b, c are in A.P., then ‘b’ is the arithmetic mean of ‘a’ and ‘c’.
Illustration 6: Insert three arithmetic means between 3 and 19.
Solution:
Difference = 19 – 3 = 16
Since three arithmetic means are to be inserted, we see that common difference d = 16/(3+1) = 4.
Hence, the required A.M. are 7, 11, and 15.
How to Prepare Arithmetic Progression Questions for CAT?
Before starting CAT Preparation for Arithmetic Progression CAT, the candidates should have complete knowledge of the following points:
- Topics covered under CAT Arithmetic Progression Questions
- The number of Arithmetic Progression Questions for CAT
- Types of the questions
Following are some tips to prepare for Arithmetic Progression CAT.
- It is suggested that the candidates should start with the basics of Arithmetic Progression for CAT first and then move on to the complicated questions.
- The candidates should regularly practice and analyse mocks and previous year’s CAT Question Papers. This will help them to solve Arithmetic Progression CAT accurately.
- The candidates need to learn multiplication tables, square roots, and cube roots for smooth calculation. This will help them to solve CAT Arithmetic Progression quickly and accurately.
![]()
===========================
Download the BYJU’S Exam Prep App NOW
The most comprehensive exam prep app.
If you are aiming to crack CAT and other MBA Exam, join BYJU’S Exam Prep Online Classroom Program where you get :
- Live Courses by Top Faculty
- Daily Study Plan
- Comprehensive Study Material
- Latest Pattern Test Series
- Complete Doubt Resolution
- Regular Assessments with Report Card
#DreamStriveSucceed

