Theory of Machines : Vibrations

Fig.1: Type of oscillating waves

Any vibrating system is a combination of:

• E storing device (i.e. mass = m)
• E storing device (having stiffness=s)
• Kinetic friction
• Unbalanced forces

1.1.     Natural Vibrations:

The vibrations in which there is no friction at all (static friction may have, but no kinetic friction) as well as there is no unbalanced force after the initial release of the system are called as “Natural Vibrations”

Fig.2: Spring-mass system

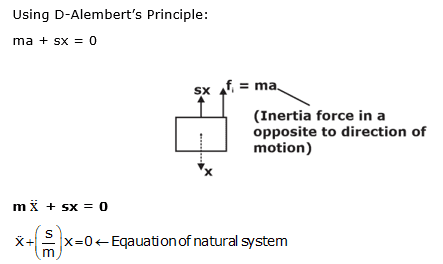
1.2.     Energy Method to calculate natural frequency:

This method is used only for natural vibrations and is used specially for Rolling problems.

In Natural Vibrations,

As, kinetic friction=0

Total energy = constant       

1.3. Torsional Vibrations:

The vibrations of a system about its own center of mass is termed as torsional vibrations.

In case of torsional vibrations, At fixed Print, as . Hence, Vibration’s amplitude will also zero. This point is called ‘Node’.

Fig.3: shaft-rotor system

1.3.1. Two-Rotor System

Fig.4: 2-rotor system

1.4.     Rayleigh’s Method to calculate natural frequency (Method of Static Deflection of Mass)

Fig.5: Basic spring Mass System

1.5.     Longitudinal-Vibrations of Beams:

• Vibrations along the length of Beam are termed as longitudinal vibrations.

Fig.6: longitudinal vibrations of a beam

1.6.     Transverse –Vibrations of Beams:

• Vibrations in a direction perpendicular to axis of the Beam.

Fig.7: Transverse vibrations of a beam

Critical Speed

• The critical speed essentially depends on
• Critical or whirling or whipping speed is the speed at which the shaft tends to vibrate violently in transverse direction.
  • The eccentricity of the C.G of the rotating masses from the axis of rotation of the shaft.
  • Diameter of the disc
  • Span (length) of the shaft, and
  • Type of supports connections at its ends.

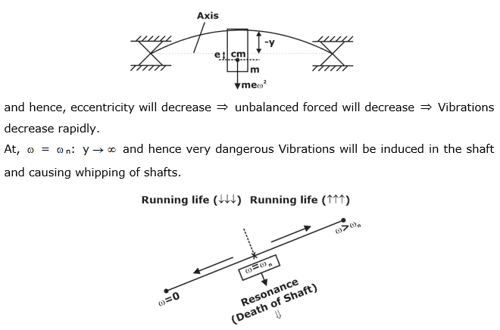
                  shaft rotor system

After Some Time

Under equilibrium:    

m(y+e) ² = sy

my ² + me ² = sy

(m ² -s) y = -me ²

1.1.   Coulomb/dry Friction Damping:

• Amplitude of Vibrations decreases with time linearly.
• Frequency and time period of oscillations do not change.
• Dissipates energy constantly because of sliding friction.
• System with friction damping is Non-linear because; frictional force always opposes Dish of Motion of the System.

1.2.   For a multi-rotor system:

If, n = no of rotors

• of natural Frequencies in n-Rotor system = (n-1)
• of node Points = (n-1).

CLICK HERE FOR 100 DAYS STUDY PLAN FOR RVUNL MECHANICAL ENGINEERING 2021

You can avail of Online Classroom Program for all AE & JE Exams:

Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses and 160+ Mock Tests)

You can avail of BYJU'S Exam Prep Test Series specially designed for all AE & JE Exams:

BYJU'S Exam Prep Test Series AE & JE (160+ Mock Tests) 

Thanks, 

Team BYJU'S Exam Prep

Sahi Prep Hai to Life Set Hai !!!