Stress and Strain is the first topic in Strength of Materials which consist of various types of stresses, strains and different properties of materials which are important while working on them.
Stress: The force of resistance per unit area, offered by a body against deformation is known as stress.

Fig.1: Stress
It is denoted by a symbol ‘σ’. And mathematically expressed as

TYPES OF STRESSES:
only two basic stresses exist.
(1) Normal stress and
(2) Shear stress.
(i) Normal stresses:
If the force applied are perpendicular or normal to areas concerned, then these are termed as normal stresses.
The normal stresses are generally denoted by a Greek letter (σ).

Fig.2 Uniaxial Normal Stress

Fig.3: Biaxial Normal Stress

Fig.4: Triaxial Normal Stress
Tensile or compressive stresses:
The normal stresses can be either tensile or compressive depending upon the direction of the load.
Sign convention: The tensile forces are termed as (+ve ) while the compressive forces are termed as negative (-ve).
(ii)Shear Stress:
when cross-sectional area of a block of material is subject to a distribution of forces which are parallel to the area concerned. Such forces are associated with a shearing of the material, are known as shear forces. The stress produced by these forces are known as shear stresses.

Fig.5: Shear stress
It is generally denoted by ‘τ’ and expressed as

The complementary shear stresses are equal in magnitude.
The same form of relationship can be obtained for the other two pair of shear stress components to arrive at the relations,
τxy=τyx
τyz=τzy
Sign convections for shear stresses:
Shear stress tending to turn the element Clockwise is taken as Positive.
Shear stress tending to turn the element Anticlockwise is taken as Negative.
STRAIN
When a prismatic bar is subjected to axial load, it undergoes a change in length, as indicated in Figure. This change in length is usually called deformation.

Fig.6: Deformation of bar under axial load
If the axial force is tensile, the length of the bar is increased, while if the axial force is compressive, there is shortening of the length of the bar.
The deformation (i.e. elongation or shortening) per unit length of the bar is termed as strain and denoted by ε or e.

Classification of strain
(i) Longitudinal strain:
The ratio of axial deformation along the length of the applied load to the original length of the body is known as longitudinal (or linear) strain.
L = Length of the body,
P = Tensile force acting on the body,
δL = Increase in the length of the body in the direction of P.
Then,

(ii) Lateral strain:
The strain at right angles to the direction of applied load is known as lateral strain. Let a rectangular bar of length L, breadth b and depth d is subjected to an axial tensile load P. The length of the bar with increase while the breadth and depth will decrease.
δL = Increase in length,
δb = Decrease in breadth, and
δd = Decrease in depth.

Fig.8: strain

(iii)Shear Strain
Change in initial right angle between two-line elements which are parallel to x and y-axis respectively.

Fig.9: Shear strain

STRESS - STRAIN DIAGRAM
The mechanical properties of a material are determined in the laboratory by performing tests on small specimens of the material, in the materials testing laboratory. The most common materials test is the tension test performed on a cylindrical specimen of the material.

Fig.16: Stress strain Diagram
A = Proportional Limit Oa = Linear Deformation
B = Elastic Limit Ob = Elastic Deformation
C = Yield Point bd = Perfect Plastic Yielding
C’ = Lower Yield Point de = Strain hardening
E = Ultimate Strength ef = Necking
F = Rupture Strength/ Fracture strength
It is customary to base all the stress calculations on the original cross-sectional area of the specimen, and since the latter is not constant, the stresses so calculated are known as Nominal stresses.
LINEAR ELASTICITY: HOOKE’S LAW
The slope of stress-strain curve is called the young’s modulus of elasticity (E):
Slope of stress-strain curve,

This equation is known as Hooke’s law.
Type of Metal Behaviour
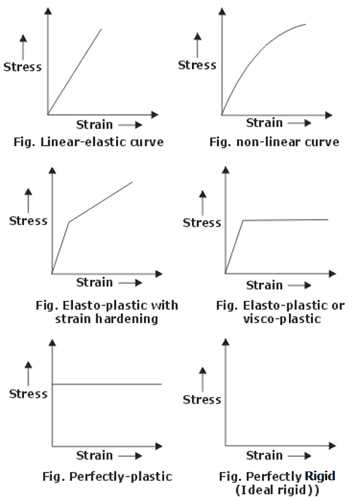
Fig.17: Stress strain Diagram
ELONGATION OF BAR UNDER DIFFERENT CONDITION
UNIFORMLY TAPERING CIRCULAR BAR
Let us now consider a uniformly tapering circular bar, subjected to an axial force P, as shown in Figure. The bar of length L has a diameter d1 at one end and d2 at the other end (d2 > d1).

Fig.18: Uniformly tapering circular bar

PRINCIPLE OF SUPERPOSITION
Bars In Series

Fig.19: A prismatic bar subjected to multiple loads
It stated that
"the resultant strain in bar will be equal to the algebraic sum of the strains caused by the individual forces acting along the length of the member.
Thus, if a member of uniform section is subjected to a number of forces, the resulting deformation (ΔL) is given by

Elastic constants
Elastic constants are those factors which determine the deformations produced by a given stress system acting on a material.
Various elastic constants are :
(i) Modulus of elasticity (E)
(ii) Poisson’s ratio (μ or 1/m)
(iii) Modulus of rigidity (G or N)
(iv) Bulk modulus (K)
Materials on the basis of elastic properties
(i)Homogeneous Material
When a material exhibits same elastic properties at any point in a given directions than the material is known as homogenous material.
(ii)Isotropic Material
When a material exhibits Same elastic properties at any direction at a given point than the material is known as Isotropic Material.
(iii)Anisotropic Material
When a material exhibits different elastic properties at every direction at a every point than the material is known as Isotropic Material.
(v) Orthotropic Material
When a material exhibits Same elastic properties at only orthogonal direction at a given point than the material is known as Orthotropic Material.
For a homogeneous and isotropic material, the number of independent elastic constants are two.
Material | No. of independent elastic constants |
Isotropic | 2 |
Orthotropic | 9 |
Anisotropic | 21 |
MODULUS OF ELASTICITY
When an axial load, P is applied along the longitudinal axis of a bar due to which length of the bar will be increases in the direction of applied load and a stress, σ is induced in the bar.
The ratio of stress to longitudinal strain, within elastic limits, is called the modulus of elasticity (E):
![]()
POISSON’S RATIO
It is the ratio of lateral strain to the longitudinal strain.
It is an unitless quantity which is generally denoted as μ or 1/m.


VOLUMETRIC STRAIN
Volumetric Strain Due to Three Mutually Perpendicular Stress
Figure shows a parallelepiped subjected to three tensile load P1, P2 and P3 in the three mutually perpendicular direction.
Then,
![]()

Fig. Parallelepiped subjected to Three Mutually Perpendicular Stress
Since any axial load produces a strain in its own direction and an opposite kind of strain in every direction at right angles to this direction.
we have,

Adding the three expressions of Equations we get.

Hydrostatic static state of stress-
In case of hydrostatic state of stress, the applied stress in all direction are equal and tensile in nature.
i.e. σ1 = σ2 = σ3 = σ

since Eϵ and σ in the above expression are positive numbers, must also be positive.

Thus, maximum value poison’s ratio is 0.5
Volumetric Strain Due to Single Direct Stress
Figure shows a rectangular bar of length L, width b and thickness t subjected to single direct load (P) acting along its longitudinal axis. Let this stress σ generated to be tensile in nature.


Fig. Volumetric strain

SHEAR MODULUS OR MODULUS OF RIGIDITY
The shear modules or modulus of rigidity expresses the relation between shear stress and shear strain.
![]()
where G = modulus of rigidity
ɸ = Shear strain (in radians) (also sometimes denoted by the symbol γ)
BULK MODULUS
When a body is subjected to three mutually perpendicular like stresses of equal intensity (σ).
Then the ratio of direct stress (σ) to the corresponding volumetric strain (ϵv) is defined as the bulk modulus K for the material of the body.
Which is generally denoted as ‘K’

RELATION BETWEEN DIFFERENT ELASTIC PROPERTIES

Value of any Elastic constant should be ≥ 0
E, K, G > 0
µ ≥ 0 [µcork = 0]
If K should be positive,
Then 1 – 2µ ≥ 0



Always
G ≤ E
For metals

You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:
BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)
You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:
BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)
Thanks
Team BYJU’S Exam Prep
Download BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.




Comments
write a comment