Strength of Materials - Torsion Complete Study Notes

Uniform Torsion

Torsion of Shaft and Combined Stresses

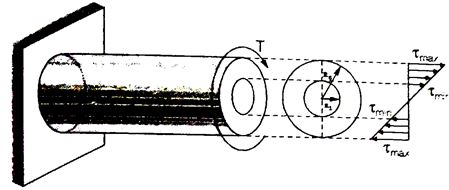
Torsion means twisting a structural Member when it is loaded by a couple that Produces rotation about the longitudinal axis.

If  τ be the intensity of shear stress, on any layer at a distance r from the centre of shaft, then

Sign Convention

• Sign convention of torque can be explained by right hand thumb rule.
• A positive torque is that in which there is tightening effect of nut on the bolt. From either side of the cross-section. If torque is applied in the direction of right hand fingers than right hand thumbs direction represents movement of the nut.

 TMD = Torsion moment diagram

T = Torque

Total angle of twist :

Where, T = Torque,

J = Polar moment of inertia

G = Modulus of rigidity,

θ = Angle of twist

L = Length of shaft,

GJ = Torsional rigidity

 Torsional stiffness;

 Torsional flexibility

 Axial stiffness

 Axial flexibility

Moment of Inertia About polar Axis:

• For solid circular shaft,: 

• For hollow circular shaft: 

Power Transmitted in the Shaft

• Power transmitted by shaft:

Where, N = Rotation per minute.

Compound Shaft

An improved type of compound coupling for connecting in series and parallel are given below

1. Series connection: Series connection of compound shaft as shown in figure. Due to series connection the torque on shaft 1 will be equal to shaft 2 and the total angular deformation will be equal to the sum of deformation of 1^st shaft and 2^nd shaft.

Therefore,

Where,

θ₁ = Angular deformation of 1^st shaft

θ₂ = Angular deformation of 2^nd shaft

1. Parallel connection: Parallel connection of compound shaft as shown in figure. Due to parallel connection of compound shaft the total torque will be equal to the sum of torque of shaft 1 and torque of shaft 2 and the deflection will be same in both the shafts. 

Therefore,

Strain energy (U) stored in shaft due to torsion:

• G = Shear modulus
• T = Torque
• J = Moment of inertia about polar axis

Effect of Pure Bending on Shaft

The effect of pure bending on shaft can be defined by the relation for the shaft,

Where, σ = Principal stress

D = Diameter of shaft

M = Bending moment

Effect of Pure Torsion on Shaft

It can be calculated by the formula, which are given below

Where, τ = Torsion

D = Diameter of shaft

Combined effect of bending and torsion

• Principal stress 

• Maximum shear stress 

• Equivalent bending moment

• Equivalent torque 

Shear Stress Distribution:

• Solid Circulation Section:

• Hollow Circulation Section

• Composite Circular Section

• Thin Tubular section: In view of small thickness-shear stress is assumed to be uniform 

You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:

BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)

You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:

BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)

Thanks

Team BYJU’S Exam Prep

Download  BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.