Sampling Theorem
The sampling process is usually described in the time domain. In this process, an analog signal is converted into a corresponding sequence of samples that are usually spaced uniformly in time. Consider an arbitrary signal x(t) of finite energy, which is specified for all time as shown in figure 1(a).
Suppose that we sample the signal x(t) instantaneously and at a uniform rate, once every TS second, as shown in figure 1(b). Consequently, we obtain an infinite sequence of samples spaced TS seconds apart and denoted by {x(NTS)}, where n takes on all possible integer values.
Thus, we define the following terms:
- Sampling Period: The time interval between two consecutive samples is referred to as the sampling period. In figure 1(b), TS is the sampling period.
- Sampling Rate: The reciprocal of the sampling period is referred to as sampling rate, i.e.
fS = 1/TS

Sampling theorem provides both a method of reconstruction of the original signal from the sampled values and also gives a precise upper bound on the sampling interval required for distortion less reconstruction. It states that
- A band-limited signal of finite energy, which has no frequency components higher than W Hertz, is completely described by specifying the values of the signal at instants of time separated by 1/2W seconds.
- A band-limited signal of the finite energy, which has no frequency components higher than W Hertz, may be completely recovered from a knowledge of its samples taken at the rate of 2W samples per second.
Aliasing & Anti-aliasing
- Aliasing is such an effect of violating the Nyquist-Shannon sampling theory. During sampling the baseband spectrum of the sampled signal is mirrored to every multifold of the sampling frequency. These mirrored spectra are called alias.
- The easiest way to prevent aliasing is the application of a steep-sloped low-pass filter with half the sampling frequency before the conversion. Aliasing can be avoided by keeping Fs>2Fmax.
- Since the sampling rate for an analog signal must be at least two times as high as the highest frequency in the analog signal in order to avoid aliasing. So in order to avoid this, the analogue signal is then filtered by a low pass filter prior to being sampled, and this filter is called an anti-aliasing filter. Sometimes the reconstruction filter after a digital-to-analogue converter is also called an anti-aliasing filter.
Explanation of Sampling Theorem
Consider a message signal m(t) bandlimited to W, i.e.
M(f) = 0 For |f| ≥ W
Then, the sampling frequency fS, required to reconstruct the bandlimited waveform without any error, is given by
Fs ≥ 2 W
Nyquist Rate
Nyquist rate is defined as the minimum sampling frequency allowed to reconstruct a bandlimited waveform without error, i.e.
fN = min {fS} = 2W
Where W is the message signal bandwidth, and fS is the sampling frequency.
Nyquist Interval
The reciprocal of Nyquist rate is called the Nyquist interval (measured in seconds), i.e.

Where fN is the Nyquist rate, and W is the message signal bandwidth.
The Z - Transform of a discrete-time signal x[n] is defined as
 , where z = r.ejω
, where z = r.ejω
- The discrete-time Fourier Transform (DTFT) is obtained by evaluating Z-Transform at z = ejω
- The z-transform defined above has both sided summation. It is called bilateral or both sided Z-transform.
Unilateral (one-sided) z-transform
- The unilateral z-transform of a sequence x[n] is defined as
![]()
Region of Convergence (ROC):
- ROC is the region where z-transform converges. It is clear that z-transform is an infinite power series. The series is not convergent for all values of z.
Significance of ROC
- ROC gives an idea about values of z for which z-transform can be calculated.
- ROC can be used to determine the causality of the system.
- ROC can be used to determine the stability of the system.
Summary of ROC of Discrete-Time Signals for the sequences

Characteristic Families of Signals and Corresponding ROC


Note: X(z) = z{x(n)} ; X1 (z) = Z {xl (n)} ; X2(z) = z{x2 (n)}; Y(z) =z (y (n))
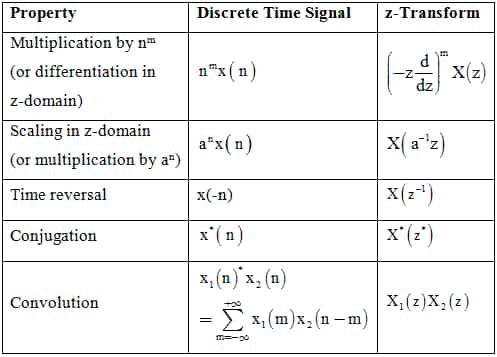
Summary of Properties of z- Transform:


Impulse Response and Location of Poles














You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:
BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)
You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:
BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)
Thanks
Team BYJU’S Exam Prep
Download BYJU’S Exam Prep APP for the best Exam Preparation, Free Mock tests, and Live Classes.




Comments
write a comment