Fourier Theorem
Any arbitrary continuous-time signal x(t), which is periodic with a fundamental period To, can be expressed as a series of harmonically related sinusoids whose frequencies are multiples of fundamental frequency or first harmonic. In other words, any periodic function of (t) can be represented by an infinite series of sinusoids called the Fourier Series.
The periodic waveform is expressed in the form of Fourier series, while a non-periodic waveform may be expressed by the Fourier transform.
The different forms of the Fourier series are given as follows.
(i) Trigonometric Fourier series
(ii) Complex exponential Fourier series
(iii) Polar or harmonic form Fourier series.
Trigonometric Fourier Series
Any arbitrary periodic function x(t) with fundamental period T0 can be expressed as follows.

This is called the trigonometric Fourier series representation of signal x(t). Here, ω0 = 2π/T0 is the fundamental frequency of x(t), and coefficients a0, an, and bn are referred to as the trigonometric continuous-time Fourier series (CTFS) coefficients. The coefficients are calculated as follows.
Fourier Series Coefficient
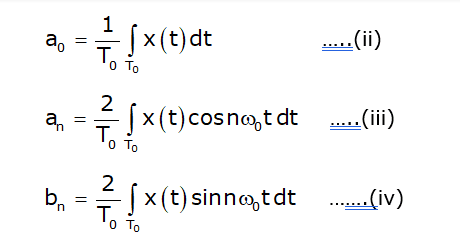
From equation (ii), it is clear that coefficient a0 represents the average or mean value (also referred to as the dc component) of signal x(t).
In these formulas, the limits of integration are either (–T0/2 to +T0/2) or (0 to T0). In general, the limit of integration is any period of the signal, and so the limits can be from (t1 to t2 + T0), where t1 is any time instant.
Trigonometric Fourier Series Coefficients for Symmetrical Signals
If the periodic signal x(t) possesses some symmetry, then the continuous-time Fourier series (CTFS) coefficients become easy to obtain. The various types of symmetry and simplification of Fourier series coefficients are disused below.
Consider the Fourier series representation of a periodic signal x(t) defined in the equation.
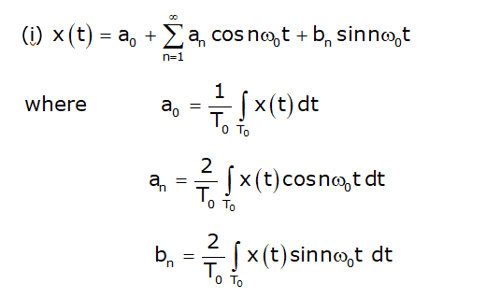
Even Symmetry: x(t) = x(–t)
If x(t) is an even function, then product x(t) sinωot is odd, and integration in equation (iv) becomes zero. That is bn = 0 for all n, and the Fourier series representation expressed as

For example, the signal x(t) shown below figure has even symmetry, so bn = 0, and the Fourier series expansion of x(t) is given as
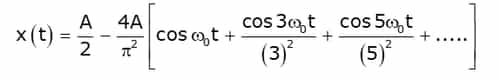
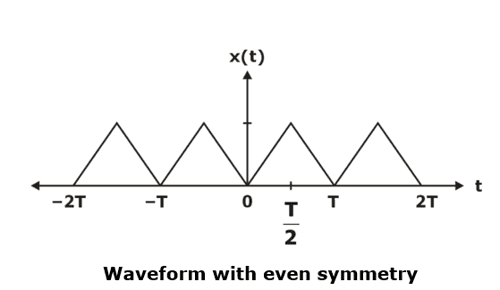
The trigonometric Fourier series representation of even signals contains cosine terms only. The constant a0 may or may not be zero.
Odd Symmetry: x(t) = –x(–t)
If x(t) is an odd function, then product x(t) cosωot is also odd and integration in equation (iii) becomes zero i.e. an = 0 for all n. Also, a0 = 0 because an odd symmetric function has a zero-average value. The Fourier series representation is expressed as

For example, the signal x(t) shown in below figure is odd symmetric, so an = a0 = 0, and the Fourier series expansion of x(t) is given as
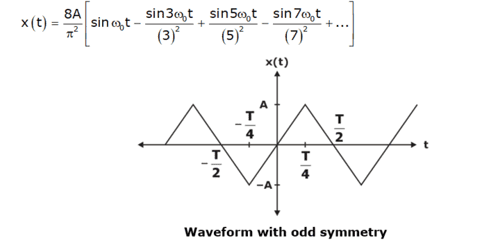
Fourier Sine Series
The Fourier Sine series can be written as
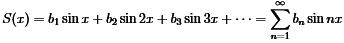 ------(2)
------(2)
- Sum S(x) will inherit all three properties:
- (i): Periodic S(x +2π)=S(x); (ii): Odd S(−x)=−S(x); (iii): S(0) = S(π)=0
- Our first step is to compute from S(x) the number bk that multiplies sin(kx).
Suppose S(x)=∑ bn sin(nx). Multiply both sides by sin(kx). Integrate from 0 to π in Sine Series in equation (2)
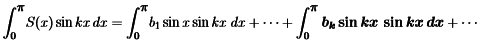
- On the right side, all integrals are zero except for n = k. Here the property of “orthogonality” will dominate. The sines make 90o angles in function space when their inner products are integrals from 0 to π.
- Orthogonality for sine Series
Condition for Orthogonality:
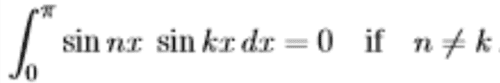 ------(3)
------(3)
- Zero comes quickly if we integrate the term cos(mx) from 0 to π. ⇒ 0∫π cos(mx) dx = 0-0=0.
- Integrating cos(mx) with m = n−k and m = n + k proves the orthogonality of the sines.
- The exception is when n = k. Then we are integrating sin2(kx) = 1/2 − 1/2 cos(2kx)
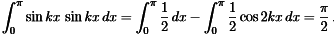
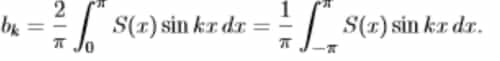 ------(4)
------(4)
- Notice that S(x)sin(kx is even (equal integrals from −π to 0 and from 0 to π).
- We will immediately consider the most important example of a Fourier sine series. S(x) is an odd square wave with SW(x) = 1 for 0<x<π. It is an odd function with period 2 π, that vanishes at x=0 and x= π.
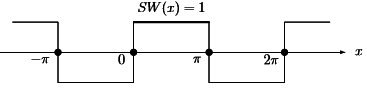
Example:
As given above, finding the Fourier sine coefficients bk of the square wave SW(x).
Solution:
For k =1,2,...using the formula of sine coefficient with S(x)=1 between 0 and π:
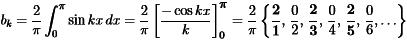
- Then even-numbered coefficients b2k are all zero because cos(2kπ) = cos(0) = 1.
- The odd-numbered coefficients bk =4/πk decrease at the rate 1/k.
- We will see that same 1/k decay rate for all functions formed from smooth pieces and jumps. Put those coefficients 4/πk and zero into the Fourier sine series for SW(x).
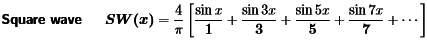
Fourier Cosine Series
The cosine series applies to even functions with C(−x)=C(x) as
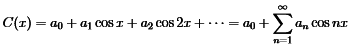 -----(5)
-----(5)
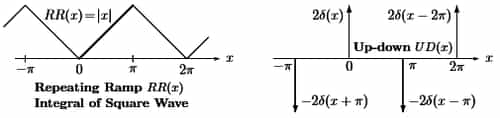
Cosine has period 2π shown as above in figure two even functions, the repeating ramp RR(x), and the up-down train UD(x) of delta functions.
- That sawtooth ramp RR is the integral of the square wave. The delta functions in UD give the derivative of the square wave. RR and UD will be valuable examples, one smoother than SW and one less smooth.
- First, we find formulas for the cosine coefficients a0 and ak. The constant term a0 is the average value of the function C(x):
![]() -----(6)
-----(6)
- We will integrate the cosine series from 0 to π. On the right side, the integral of a0=a0π (divide both sides by π). All other integrals are zero.
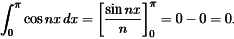
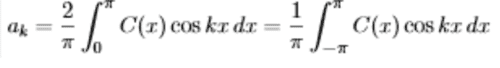
- Again the integral over a full period from −π to π (also 0 to 2π) is just doubled.
Orthogonality Relations of Fourier Series
Since from the Fourier Series Representation, we concluded that a periodic Signal it could be written as
 -------(7)
-------(7)
The condition of orthogonality is as follows:
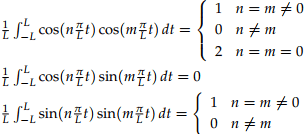
Proof of the orthogonality relations:
This is just a straightforward calculation using the periodicity of sine and cosine and either (or both) of these two methods:
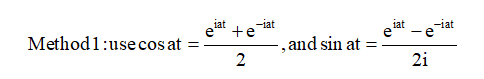
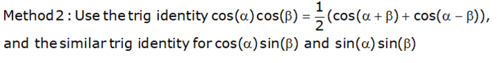
Energy in Function = Energy in Coefficients
There is also another important equation (the energy identity) that comes from integrating (F(x))2. When we square the Fourier series of F(x) and integrate from −π to π, all the “cross-terms” drop out. The only nonzero integrals come from 12 and cos2 kx and sin2 kx, multiplied by a02,ak2 bk2.
- Energy in F(x) equals the energy in the coefficients.
- The left-hand side is like the length squared of a vector, except the vector is a function.
- The right-hand side comes from an infinitely long vector of a’s and b’s.
- If the lengths are equal, which says that the Fourier transforms from function to vector is like an orthogonal matrix.
- Normalized by constants √2π and √π, we have an orthonormal basis in function space.
Complex Fourier Series
- In place of separate formulas for a0 and ak and bk, we may consider one formula for all the complex coefficients ck.
- So that the function F(x) will be complex, The Discrete Fourier Transform will be much simpler when we use N complex exponentials for a vector.
The exponential form of the Fourier series of a periodic signal x(t) with period T0 is defined as
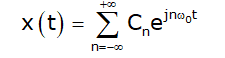
where ω0 is the fundamental frequency given as ω0 = 2π /T0. The exponential Fourier series coefficients cn are calculated from the following expression
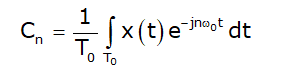
- Since c0 = a0 is still the average of F(x), because e0 = 1.
- The orthogonality of einx and eikx is to be checked by integrating.
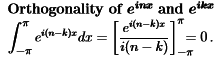
Example:
Compute the Fourier series of f(t), where f(t) is the square wave with period 2π. defined over one period.
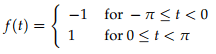 The graph over several periods is shown below.
The graph over several periods is shown below.
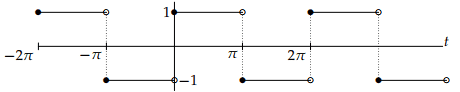
Solution:
Computing a Fourier series means computing its Fourier coefficients. We do this using the integral formulas for the coefficients given with Fourier’s theorem in the previous note. For convenience, we repeat the theorem here.
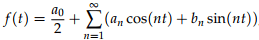
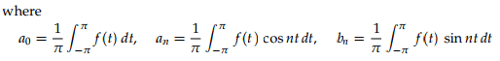
By applying these formulas to the above waveform, we have to split the integrals into two pieces corresponding to where f(t) is +1 and where it is −1.
thus for n ≠ 0 ; 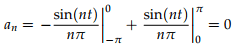
for n = 0 ![]()
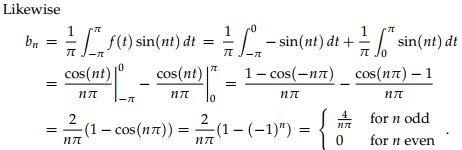
We have used the simplification cos nπ = (−1)n to get a nice formula for the coefficients bn.
This then gives the Fourier series for f(t)
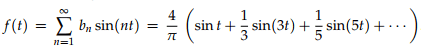
Fourier Transform:
Fourier transform is a transformation technique that transforms non-periodic signals from the continuous-time domain to the corresponding frequency domain. The Fourier transform of a continuous-time non-periodic signal x(t) is defined as
![]()
where X(jω) is the frequency domain representation of the signal x(t), and F denotes the Fourier transformation. The variable ‘ ω’ is the radian frequency in rad/sec. Sometimes X(jω) is also written as X(ω).
If the frequency is represented in terms of cyclic frequency f (in Hz), then the above equation is written as
![]()
Note:
The signal x(t) and its Fourier transform X(jω) are said to form a Fourier transform pair denoted as
![]()
Existence of Fourier Transform:
A function x(t) has a unique Fourier transform if the following conditions are satisfied, which are also referred to as Dirichlet Conditions:
Dirichlet Conditions:
(i) is absolutely integrable. That is,
![]()
(ii) x(t) has a finite number of maxima and minima and a finite number of discontinuities within any finite interval.
The above conditions are only sufficient conditions but not necessary for the signal to be Fourier transformable. For example, the signals u(t),r(t), and cos (ω0t) are not absolutely integrable but still possess a Fourier transform.
Magnitude and Phase Spectrum:
The Fourier transform X(jω) of a signal x(t) is, in general, the complex form that can be expressed as
![]()
The plot of |X(jω)| versus ω is called the magnitude spectrum of x(t), and the plot of ![]() versus ω is called the phase spectrum. The amplitude (magnitude) and phase spectra are together called Fourier spectrum, which is nothing but the frequency response of X(jω) for the frequency range
versus ω is called the phase spectrum. The amplitude (magnitude) and phase spectra are together called Fourier spectrum, which is nothing but the frequency response of X(jω) for the frequency range ![]() .
.
Inverse Fourier Transform:
The inverse Fourier transform of X(jω) is given as
![]()
This method of calculating the inverse Fourier transform seems difficult as is involves integration. There is another method to obtain inverse Fourier transform using partial fraction. Let a rational Fourier transform is given as
![]()
X(jω) can be expressed as a ratio of two factorized polynomials in jω as shown below.

By partial fraction expansion technique, the above can be expressed as shown below.
![]()
where k1 ,k2 ......kn calculated depending on whether the roots are real and simple or repeater or complex.
Properties of Fourier Transform:
There are some properties of continuous-time Fourier transform (CTFT) based on the transformation of signals, which are listed below.
a. Linearity:
The linearity property states that the linear combination of signals in the time domain is equivalent to a linear combination of their Fourier transform in the frequency domain.

where a and b are any arbitrary constants.
b. Time Shifting:
The time-shifting property states that the delay of t0 in the time domain is equivalent to multiplication of ![]() with its Fourier transform. It implies that the amplitude spectrum of the original signal does not change, but the phase spectrum is modified by a factor of -jωt0.
with its Fourier transform. It implies that the amplitude spectrum of the original signal does not change, but the phase spectrum is modified by a factor of -jωt0.

c. Conjugation and Conjugate Symmetry:

d. Time Scaling
Time scaling property states that the time compression of a signal in the time domain is equivalent to expansion in the Frequency domain and vice-versa,

e. Differentiation in Time-Domain
The time differentiation property states that differentiation in the time domain is equivalent to the multiplication of jω in the frequency domain.

f. Integration in Time-Domain:

g. Differentiation in Frequency Domain:
The differentiation of Fourier transform in the frequency domain is equivalent to the multiplication of time-domain signal with -jt .
Differentiation in Frequency Domain


h. Frequency Shifting:
The frequency-shifting property states that a shift of ω0 in frequency is equivalent to multiplying the time domain signal by ![]()

i. Duality Property:

j. Time Convolution:
Convolution between two signals in the time domain is equivalent to the multiplication of Fourier transforms of the two signals in the frequency domain.

k. Frequency Convolution:
Convolution in the frequency domain (with a normalization factor of 2π) is equivalent to multiplying the signals in the time domain.

l. Area Under x(t):
If X(jω) is the Fourier transform of x(t), then,
![]()
that is, the area under a time function x(t) is equal to the value of its Fourier transform evaluated at ω= 0
m. Area Under X(jω):
If X(jω) is the Fourier transform of x(t), then,

n. Parseval's Energy Theorem:
If X(jω) is the Fourier transform of an energy signal x(t). then
![]()
where Ex is the total energy of the signal x(t).




Comments
write a comment