Signals & Systems - Laplace Transform Complete Study Notes

Laplace Transform

The Laplace Transform is a very important tool to analyse any electrical containing by which we can convert the Integral-Differential Equation in Algebraic by converting the given situation in Time Domain to Frequency Domain

•  is also called bilateral or two-sided Laplace transform.
• If x(t) is defined for t≥0, [i.e., if x(t) is causal], then  is also called unilateral or one-sided Laplace transform.

Below we have listed the Following advantage of accepting Laplace transform:

• Analysis of general R-L-C circuits become easier.
• Natural and Forced response can be easily analyzed.
• The circuit can be analyzed with impedances.
• Analysis of stability can be done easiest way.

Statement of Laplace Transform

• The direct Laplace transform or the Laplace integral of a function f(t) defined for 0 ≤ t < ∞ is the ordinary calculus integration problem for a given function f(t).
• Its Laplace transform is the function, denoted F(s) = L{f}(s), defined by
  

• A causal signal x(t) is said to be of exponential order if a real, positive constant σ (where σ is the real part of s) exists such that the function, e^{- σt}|X(t)| approaches zero as t approaches infinity.
• For a causal signal, if lim e^-σt|x(t)|=0,  for σ > σ_c and if lim e^-σt|x(t)|=∞ for σ > σ_c then σ_c is called the abscissa of convergence, (where σ_c is a point on real axis in s-plane).
• The value of s for which the integral  converges is called Region of Convergence (ROC).
• For a causal signal, the ROC includes all points on the s-plane to the right of abscissa of convergence.
• For an anti-causal signal, the ROC includes all points on the s-plane to the left of the abscissa of convergence.
• For a two-sided signal, the ROC includes all points on the s-plane in the region in between two abscissae of convergence.

Properties of the ROC

The region of convergence has the following properties

• ROC consists of strips parallel to the jω-axis in the s-plane.
• ROC does not contain any poles.
• If x(t) is a finite duration signal, x(t) ≠ 0, t₁ < t < t₂ and is absolutely integrable, the ROC is the entire s-plane.
• If x(t) is a right sided signal, x(t) = 0, t₁ < t₀, the ROC is of the form R{s} > max {R{p_k}}
• If x(t) is a left sided signal x(t) = 0, t₁ > t₀, the ROC is of the form R{s} > min {R{p_k}}
• If x(t) is a double-sided signal, the ROC is of the form p₁ < R{s} < p₂
• If the ROC includes the jω-axis. Fourier transform exists and the system is stable.

Inverse Laplace Transform

• It is the process of finding x(t) given X(s)

X(t) = L^-1{X(s)}

      There are two methods to obtain the inverse Laplace transform.

• Inversion using Complex Line Integral

• Inversion of Laplace Using Standard Laplace Transform Table.

Note A: Derivatives in t → Multiplication by s.

 B: Multiplication by t → Derivatives in s.

Laplace Transform of Some Standard Signals

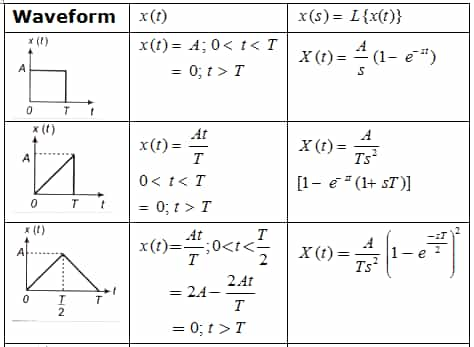
 Some Standard Laplace Transform Pairs

Properties of Laplace Transform

Key Points

• The convolution theorem of Laplace transform says that Laplace transform of convolution of two time-domain signals is given by the product of the Laplace transform of the individual signals.
• The zeros and poles are two critical complex frequencies at which a rational function of a takes two extreme value zero and infinity respectively.

You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:

BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)

You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:

BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)

Thanks

Team BYJU’S Exam Prep

Download  BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.