The existence of solids in nature occurs principally in two forms: crystalline and non-crystalline (amorphous), which differ substantially in their properties.
Crystals are solids that possess long-range order. There is a long-range order in crystalline solids, a regular pattern of arrangement of particles that repeats itself periodically can be seen over the whole crystal. Excluding the defects that can arise during the crystal growth, the arrangement of the atoms at one point in a crystal is identical to that in any other part of the crystal.
Determination of the number of ways in which the component atoms are arranged in crystals and how the long-range order may be achieved is done using crystallography. Many physical and chemical properties are dependent on crystal structure and therefore the knowledge of crystallography is necessary if the properties of materials are to be understood and exploited.
Space Lattices- A space lattice provides the framework with reference to which a crystal structure can be described. An infinite array of points in three dimensions in which every point has a surrounding identical to that of every other point in the array termed as a space lattice.
UNIT CELL- A unit cell is the smallest component of the space lattice. The unit cell is the fundamental building block or structural unit of the crystal structure because of its geometry and atomic positions.
Lattice parameters of a unit cell- The unit cell is formed by primitives or intercepts a, b and c along X, Y and Z axes respectively. The three angles α, β and γ are called interfacial angles. One can easily determine the form and actual size of the unit cell if the values of these intercepts and interfacial angles are known.
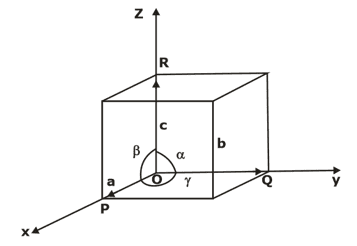
PRIMITIVE CELL- A geometrical shape which, when repeated indefinitely in 3-dimensions, will fill all space and is equivalent of one lattice point is termed as the primitive cell. All the primitive cells need not to be unit cells but the reverse could be true.
CRYSTAL FAMILIES AND CRYSTAL SYSTEMS- If all the atoms at the lattice points are identical, the lattice is said to be Bravais lattice. Crystals could be classified in terms of six crystal families, called anorthic, monoclinic, orthorhombic, tetragonal, hexagonal and iso-metric only upon careful measurement of the mineral specimen. A little expansion of this classification has been done by crystallographers. The crystal systems are sets of reference axes, which have a magnitude as well as a direction, and therefore are vectors.
Crystal family | Crystal system | Axial relationships | Lattice type | Examples |
Isometric | Cubic | a = b = c and | P, F, C | Au, NaCl, CaF2, CrCl, CaO (I) |
Tetragonal | Tetragonal | a = b ≠ c and | P, C | NiSO4, Sn, TiO3, and SnO2 |
Orthorhombic | Orthorhombic | a ≠ b ≠ c and | P, B, F, C | MgSO4, KNO3, and BaSO4 |
Monoclinic | Monoclinic | a ≠ b ≠ c and | P, B | 2H2O, NaSO4, CaSO4, FeSO4 |
Anorthic | Triclinic | a ≠ b ≠ c and | P | K2Cr2O7, CuSO4, K2S2O8 |
Hexagonal | Hexagonal | a = b ≠ c and | P | AgCl2, Sio2, Zn and Graphite |
| Rhombohedral | a’ = b’ ≠ c’ and (Hexagonal axes) | P or R | SiO2, CaSO4, and CaCO3 |
Representation of symbols:
P → primitive,
B → base centred
C → body centred
F → face centred
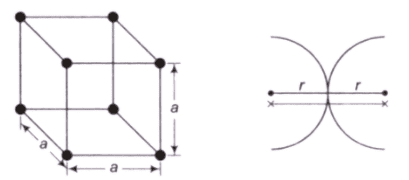
Atomic radius- This is defined as half the distance between the nearest neighbours in the crystal structure of a pure Atomic radius is denoted by r and expressed in terms of the cube edge element a.
Atomic Packing Factor (APF)-The ratio of total volume of all the atoms in one unit cell to the whole volume of the unit cell (also called relative density of packing (RDP)) is known as Atomic Packing Factor.
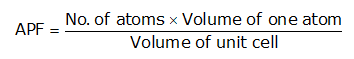
DENSITY OF CRYSTAL- This is defined as:
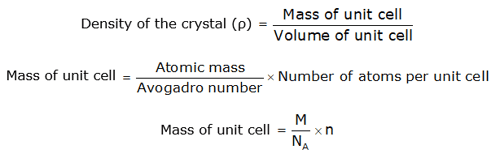
Where:
number of atoms in a unit cell and → n
Avogadro's number → NA
the atomic weight, and →M
side of a cubic unit cell → a
![]()
DIRECTIONS, LATTICE PLANES AND MILLER INDICES- There exists lattice and directions planes in a crystal which contain a large concentration of atoms. Different properties of crystals, particularly mechanical properties are related to the structure of the crystal though the help of crystal directions.
- Crystal Directions: To specify the direction of a straight-line joining lattice points in a crystal lattice, we choose any lattice point on the line as the origin and the vector connecting this to any other lattice point on the line.
- Crystallographic Planes: The crystal lattice may be considered to made of an aggregate of a set of equidistant parallel planes, passing through the lattice points, which are known as lattice planes, or atomic planes.
- Miller indices of a direction are simply the vector components of the direction resolved along each of the coordinate’s axis, expressed as multiples of the unit cell parameters and reduced to their simplest form. They are denoted by [hkl].
- Miller indices of the plane a method to designate a set of parallel planes in a crystal by three' numbers h, k and l usually written within brackets by (h k l).
- Interplanar spacings: Distances between different planes are shown by a number of parts of the body diagonal of a unit cell. The distance between planes can be calculated as per the miller indices as follows, (In a cubic system: a = b = c)
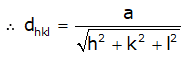
CO-ORDINATION NUMBER- The number of nearest atoms directly surrounding the particular atom. It is 6 for simple cubic, 8 for BCC and 12 for FCC. For closely packed structures, the value of this number is 12.
- For carbon atoms, the value of coordination number is 4, i.e. it has 4 nearest neighbours. The low coordination results in a comparatively less efficient packing of the carbon atoms in the crystal.
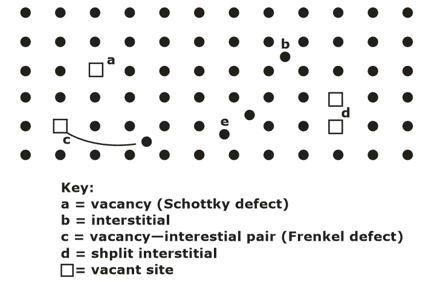
DEFECTS OR IMPERFECTIONS IN CRYSTALS- In ideal crystals atoms were arranged in a regular way. Certain defects or imperfections are always present in real crystals, and therefore, the arrangement of atoms in the volume of a crystal is far from being perfectly regular. Based on geometry, crystalline defects can be classified as :
- Point imperfections- The point imperfections, which are lattice errors at isolated lattice points, take place due to the imperfect packing of atoms during crystallization.
- Vacancies
- Interstitial Imperfections
- Frenkel defect
- Schottky Defect
- Substitutional Defect
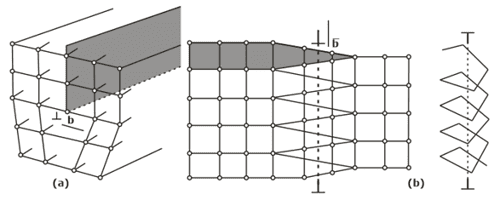
- Line imperfections- A dislocation is a linear disturbance (1 D) imperfection in a geometrical sense of the atomic arrangement occurring on the slip plane through the crystal.
- Edge Dislocation
- Screw Dislocation
- Climb Dislocation
- Surface and grain boundary imperfections
- Volume imperfections
Simple Cubic Cell (SCC)- In a SCC, there is an atom present at each corner of the cell and the centres of these atoms coincide with each corner.

- (1/8)th part of the atom is present in the cell. The total number of atoms present in crystal structure is 1
- r + r = a, Where r = Atomic radius, a = Lattice constant.
- Percentage APF = 52%
- Percentage of voids can be calculated as : 100 – 52 = 48%

- Total effective number of atoms present in the crystal is 2
- Percentage APF = 68%
- Percentage of voids can be calculated as: 100 – 68 = 32%
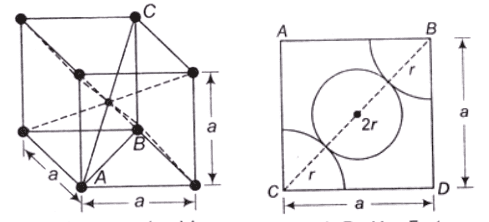
Face Centred Crystal (FCC)- In FCC, each face has an atom and atoms are also present at the corners of the unit cell.
- Total effective number of atoms in cell is 4
- Percentage APF = 74%
Percentage of voids can be calculated as: 100 – 74 = 26%You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:
BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)
You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:
BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)
Thanks
Team BYJU’S Exam Prep
Download BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.




Comments
write a comment