In this article, you will find the Study Notes on Electrostatics which will cover the topics such as Force of interaction between two charged particles, Electric Field due to Infinite Line Charge, Electric Field due to Uniformly Charged Ring, Electric Field due to Infinite Sheet of Charge, Superposition Principle of Fields, Electric Flux, Electric Potential, Dipole Moment, Electric flux lines and Electric field due to Dipole etc
- Coulomb’s Law describes the electrostatic interaction between two charged particles.
- It can be derived by combining the equation for the electric field around a spherical charge.
- According to Coulomb's law, the force acting between two point charges is:
- directly proportional to the magnitude of each charge,
- inversely proportional to the square of the separation between their centres, and
- directed along the separation vector connecting their centres.
- The force acting between two electric charges is radial, inverse-square, and proportional to the product of the charges.
- It is an inverse-square law, given by:
(OR)
F12= (ke Q1 Q2) / r2

- where Q1 and Q2 are the magnitudes of the two charges respectively and r is the distance between them, F12 is the force on particle 1 from particle 2, ke is called as Coulomb's constant (ke = 8.99×109 N m2 C-2), and ε0 is vacuum permittivity (8.85 × 10−12 C2/Nm2).
- F12 = –F21 and |F12| = |F21|, it means that force acting on charge Q2 due to Q1 is always equal to the force acting on charge Q1 due to Q2 magnitude but opposite in direction.
- The signs of Q1 and Q2 must be taken into account means for the same polarity charges Q1Q2 > 0 and for opposite polarity charges Q1Q2 < 0.
- Coulomb’s force obeys the law of superposition.
- Note that when both particles have the same sign of charge then the force is in the same direction as the unit vector and the particle is repelled.
- The SI unit of electric charge is the coulomb (C)
Force per unit charge is called electric field intensity
line charge :
![]()
Where ρL is line charge density in C/m and r is radial distance.
surface charge :
![]()
Where ρS is surface charge density in C/m2 and an is unit vector normal to the plane containing the sheet.
Electric Field due to Infinite Line Charge

Consider an infinitely long straight line carrying uniformly line charge having density ρL C/m.
The electric field intensity at point P.
![]()
Electric Field due to Uniformly Charged Ring
Consider a charged circular ring of radius r placed in XY plane with centre at the origin. Carrying a charge uniformly along its circumference. The charge density is ρL C/m.
Electric Field due to Infinite Sheet of Charge
Consider an infinite sheet of charge having uniform surface charge density ρs C/m2, placed in XY plane. We want to find E at point P present at the z-axis.
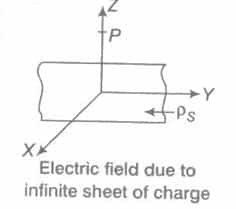
![]()
Superposition Principle of Fields
The electric field of a point charge is a linear function of the value of the charge. The fields of more than one point charge are linearly superimposable by vector addition. This is the principle of superposition applied to the electric field and states that the total resultant field at a point is the vector sum of the individual components of the field at the point.
Electric Flux
It may be defined as
![]()
Where D is electric flux density and it can be given as
D = ε0 E = Electric flux density (C/m2)
where, ε0 = Permittivity of the vacuum = 8.854 × 10–12 F/m
Electric Potential
The Work was done per unit charge or potential energy per unit charge is known as potential difference.

Electric field intensity can be given as the negative potential gradient of electric field i.e,
E = -∇V
The electric field is irrotational or conservative in nature i.e., ∇ × E = 0
Note: Electric dipole is formed when two points charged of equal magnitudes and opposite polarities are separated by a small distance.
Dipole Moment
p = Q d Coulomb-meter
where, d is the distance vector from –Q to Q.
Electric field Intensity at a Point due to a Dipole
An electric dipole or simply a dipole consists of two point charges of equal magnitude and opposite sign, separated by a very small distance.

Field due to Dipole
The field due to a dipole at a very large distance from the dipole.
![]()
where, p = Ql
and ar, aθ = Unit vectors
| S.No. | Charge | Electric Field | Potential |
| 1 | One point charge (monopole) |  |  |
| 2 | Two-point charge (dipole) |  |  |
| 3 | Three-point charge (tripole) |  |  |
| 4 | Four-point charge (quadruple) |  |  |
Electric Flux
The electric field at any distance r from a point charge in free space.
![]() Newton/Coulomb
Newton/Coulomb
![]()

With E as a vector in free space, ε0E is designated by a symbol D; called electric flux density
D = ε0 E
The integral of the normal component of the vector D over a surface is defined as the electric flux over the surface.
Electric Flux Lines
An electric flux line is an imaginary path or line which is drawn in such a way that its direction at any point is the same as the direction of the electric field at that point. The electric flux density (D) is always tangential to electric flux lines. Electric flux lines are also called electric lines of force.

Electric field emanates (or originates) from a positive and terminates (or ends) on a negative charge.
An equipotential surface is a surface on which potentially remains the same throughout the surface and there is no potential difference. The flux line or force line for an equipotential surface is known as an equipotent line on equipotential surfaces or equipotential lines, the potential difference between any points A and B is always zero.
Electrostatic Energy Density

Introduction to Gauss's law for a conductor and example on Gauss's Law Applications and Divergence of the flux density, electric field and potential.
- The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.
- Total electric flux y through any closed surface is equal to the total charge enclosed by that surface.
- Gauss’s Law helps us understand the behaviour of electric fields inside the conductors.
- The Gauss law also helps us understand the distribution of electric charge placed on a conductor.
- The area integral of the electric field over any closed surface is equal to the net charge enclosed in the surface divided by the permittivity of space.
- Gauss' law is a form of one of Maxwell's equations.
![]()
![]()
![]()
(Maxwell’s first equation)
- Net flux through a surface is equal to the net charge enclosed by the volume occupied by the surface.

Where, rV = Volume charge density
- Total charge enclosed:

- Gauss’s law is an alternative statement of Coulomb’s law. Proper application of the divergence theorem to Coulomb’s law results in Gauss’s law.
- Coulomb’s law is applicable in finding the electric field due to any charge configuration but Gauss’s law is applicable when charge distribution is symmetrical.
Divergence of the Flux Density
Let E be a simple solid region and S is the boundary surface of E with positive orientation.
Let D be a vector field whose components have continuous first-order partial derivatives.
Then, the divergence of a vector field D is defined at any point as



(Gauss’s law in differential form)
(Gauss’s law in integral form)
You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:
BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)
You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:
BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)
Thanks
Team BYJU’S Exam Prep
Download BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.






Comments
write a comment