Digital Electronic - Sequential Logic Circuits Complete Study Notes

1. Introduction

The sequential circuit is of two types.

• Synchronous Sequential Circuit: Change in input signals can affect memory elements only upon activation of clock signals.
• Asynchronous Sequential Circuit: Change in input signals can affect memory elements at any instant of time. These are faster than the synchronous circuit.

2. Flip Flops

• It is a one-bit memory cell which stores the 1-bit logical data (logic 0 or logic 1).
• It is a basic memory element.
• The most commonly used application of flip flops is in the implementation of a feedback circuit.
• As a memory relies on the feedback concept, flip flops can be used to design it.
• In the synchronous sequential circuit, Memory elements are clocked flip flops and generally edge triggered.
• In the asynchronous sequential circuit, Memory elements are unclocked flip flops/time delay elements which are generally level triggered.
• Flip flop circuit is also known as bistable multivibrator or latch because it has two stable states (1 state, 0 states).

For the electronic circuits, there are mainly four types of flip flops present.

• S-R Flip Flop (Basic Flip Flop)
• Delay Flip Flop (D Flip Flop)
• J-K Flip Flop
• T Flip Flop

Basic SR Flip Flop

• The Set-Reset (SR) flip flop is designed with the help of two NOR gates or two NAND gates.
• SR Flip Flop is also called as SR latch.

SR Latch Implementation Using NAND Gates:

Logic diagram of SR latch using NAND gates

Truth Table of Logic Diagram

SR Latch Using NOR Gates:

Logic diagram of SR latch using NOR gates

Truth Table of Logic Diagram

Clocked SR Flip Flop Implementation using NAND Gates:

It is also called a Gated S-R flip flop. The main problem with S-R flip flops is using NOR and NAND gate in the invalid state. By using a bistable SR flip-flop this problem can be overcome. This can change outputs when certain invalid states are met, regardless of the condition of either the Set or the Reset inputs.

• SR Flip Flop Using NOR Gates:

SR flip flop using NOR gates

Truth Table of SR Flip Flop

With both S=1 and R=1, the occurrence of a clock pulse causes both outputs to momentarily go to 0. When the pulse is disabled (removed), the state of the flip-flop become indeterminate, depending on whether the set or reset input of the flip-flop remains at 1 longer than the transition to 0 at the end of the pulse.

Characteristic Table

Characteristic equation of SR flip flop

Excitation Table

JK Flip Flop

A JK flip-flop eliminates the indeterminate state of the SR type. Inputs J and K is similar to the inputs S and R to set and clear the flip-flop (In JK flip-flop, the letter J is set and the letter K is for clear). When logic 1 are applied to both J and K inputs simultaneously, the flip-flop switches to its complement state. If Q=1 then it switches to Q=0 and vice versa.

• JK flip flop using SR flip flop:

S = JQ'

R = KQ

• JK flip flop using NAND latch:

• JK flip flop using NOR latch:

Characteristic Table

Excitation Table

• Characteristic equation for JK flip flop:

D-Flip Flop

D flip flop is also known as a Transparent latch, Delay flip flop or data flip flop. The D input goes directly to the S (J) input and the complement of the D input goes to the R (K) input. 

• The D-flipflop has only a single data input (D).
• If D = 1, the flip-flop is switched to the set state (unless it was already set).
• If D = 0, the flip-flop switches to the clear state.

Truth Table

Characteristic Table

Excitation Table

• Characteristic equation for D-flop flop

Q_{n + 1} = D

T – Flip Flop

• The T flip-flop is a single input version of the JK flip-flop where T is connected to both J and K inputs directly.
• When T = 0, the flip flop enters into Hold mode, which means that the output, Q is kept the same as it was before the clock edge.
• When T = 1, the flip flop enters into Toggle mode, which means the output Q is negated after the clock edge, compared to the value before the clock edge.

Truth Table

Characteristic Table

Excitation Table

• The characteristic equation of T-Flip Flop:

Q_{n + 1} = T ⊕ Q_n

• Race Around Condition:
  • The race around condition will occur in JK flip flop when J = K = 1 and t_pd (FF) < t_pw.
  • To avoid race around condition.

t_pw < t_pd (FF) < T_CLK

3. Master Slave (MS) Flip Flop

• A master-slave flip-flop is constructed from two separate flip-flops. One circuit serves as a master and the other as a slave. Input clock is applied to master and Inverted clock applied to slave.

• In Master Slave, flip flop output is changed only when slave output is changing.
• The master flip-flop is enabled on the positive edge of the clock pulse and the slave flip-flop is disabled by the inverter.
• The information at the external J and K inputs is transmitted to the master flip-flop.
• When the pulse returns to 0, the master flip-flop is disabled and the slave flip-flop is enabled. The slave flip-flop then goes to the same state as the master flip-flop.
• Master is level triggered, and Slave is edge triggered
• No race around condition occurs in Master Slave flip flop.
• It stores only one bit.

4. Flip Flop Conversions

The flip flop conversions are classified into different types which are:

• SR-FF to JK-FF Conversion
• JK-FF to SR-FF Conversion
• SR-FF to D-FF Conversion
• D-FF to SR-FF Conversion
• JK-FF to T-FF Conversion
• JK-FF to D-FF Conversion
• D-FF to JK-FF Conversion

Procedure for Flip Flop conversion:

1. Conversion Table: Construct the characteristic table of required flip flop (unknown), and fill available (known) flip flop excitation.
2. Solve K map for given (known) flip flop as input and required flip flop as output.
3. Implement the required flip flop using the known flip flop.

Example: Conversion from JK flip flop to D flip flop is shown below.

Characteristic Table

5. Registers

When a group of the flip flop is used to store a word ( a group of bits) then it is called register. To store n bits, n flip flops are cascaded in the register. If in a register, the binary information can be moved from stage to stage, this type of registers is called shift registers. According to data movement in a register, shift registers can be classified as

• Serial Input Serial Output (SISO)
• Serial Input Parallel Output (SIPO)
• Parallel Input Serial Output (PISO)
• Parallel Input Parallel Output (PIPO)

Serial Input Serial Output (SISO)

• In registers edge trigger circuit used to make circuit synchronous.
• If no clock is applied then get same data which is stored.
• In N bits SISO registers to provide N bits data, Serially in require N clock pulse, and Serially out require (N-1) clock pulse.

Serial Input Parallel Output (SIPO)

• To provide N-bit data: Serial in requires N clock pulse, and Parallel out requires no clock pulse.
• SIPO can provide n × t_CIK delay to the input.
• SIPO can convert serial data or temporal code to parallel or serial code.

Parallel Input Serial Output (PISO)

• If control = 0 then it acts as parallel input;
• If control = 1 then it acts as serial output;
• To provide parallel input, one clock pulse is required.
• To provide N bits serial output, it requires (N-1) clock pulse.
• PISO can convert special code to temporal code.

Parallel Input Parallel Output (PIPO)

• In PIPO register for parallel input number of pulse required is 1 clock pulse.
• In PIPO register for parallel output number of pulse required is 0 clock pulse.
• PIPO register cannot be used as a shift register.
• It is used for temporal storage of data in microcontroller, DSP, CPU etc.

Summary of Registers

6. Counter

• A counter is a sequential logic circuit capable of counting the number of clock pulses arriving at its clock input.
• The sequence of count may be ascending, descending or non-sequence.
• For a counter circuit having n flip flops, Maximum possible states (N) = 2ⁿ
• If N = 2ⁿ , the counter acts as a binary counter.
• If  N < 2ⁿ  , the counter the non-binary counter.
• It counter is capable to count from 0 to 2ⁿ-1.
• MOD number is the Number of states present in a counter is known as modulus count or MOD number.
• For n-flip flops, the counter will have 2ⁿ different states then this counter is said MOD- 2ⁿ counter.

MOD-N Counter

• MOD number indicates frequency division obtained from the last flip flops.

• Cascaded two counters:

• MOD-MN counter:
  • Overall states of combined counter = MN
  • Input frequency = f
  • Output frequency f = f/(MN)

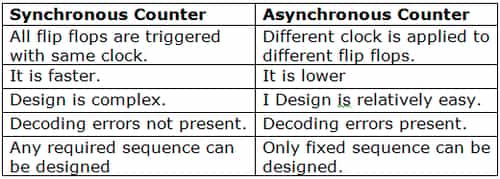
7. Classification of Counters

Based upon the applying clock pulse, counters are classified into two categories.

• Synchronous counter
• Asynchronous counter (ripple counter)

8. Toggle Mode Circuit

These are frequency dividers circuit.

Other Toggle Mode Circuit

9. Asynchronous Counter (Ripple counter)

• A different clock pulse is applied to different flip flops.
• All flip flops are operating in toggle mode.
• In asynchronous counter flip flop applied with external clock acts as LSB bit.

3-bit Ripple Up Counter

• Input clock is applied at LSB bit.
• It n-bit ripple counter maximum possible states are 2ⁿ.
• Bit ripple up counter counts from 0 to 2^{n - 1}.
• If all states are used then with input frequency f, then output frequency will be f/2ⁿ
• Calculation of Time Period of Flip Flop: In n-bit ripple counter if propagation delay of each flip flop is t_pd(FF), then the time period of the clock is:

• Maximum Clock Frequency:

• Due to propagation delays of flip flops decoding errors are present.
• Clear and preset are known as asynchronous input to flip flop.
• In any ripple counter, the following conditions will fulfil
  • Negative edge trigger and Q as clock ⇒ up counter
  • Positive edge trigger and Q as clock ⇒ up counter

3-bit Ripple Down Counter

• Positive edge trigger and Q as clock ⇒ down counter
• Negative edge trigger and Q as clock ⇒ down counter

Non-binary Ripple Counter

Decode counter or BCD counter is an example of a non-binary counter. It requires 4 flip flops.

• Used state = 10 and unused states = 6 → (2⁴ -10)
• Output frequency of BCD counter = f/10
• For making non-binary counter clear (clr) signal is used.
• c1r is active high, and (clr)' is active low.

10. Synchronous Counters

In this type of counter, there are no connections of the first flip flop output to a clock input of the next flip flop.

Ring Counter: It is a circular shift register with only flip flop being set at any particular time, all others are cleared. It is a shift register with feedback.

• In-ring counter, if the feedback is used the number of states is reduced.
• With n flip flops maximum states = n.
• Number of unused states in-ring counter = 2ⁿ – n
• Maximum Clock Frequency: If the input frequency is f, then at the output of every flip flop we get f/N frequency. In-ring counter, if the propagation delay of each flip flop is t_pd(FF) then

Johonson Ring Counter: Jhonson ring counter is also called as a Twisted ring counter, Switch tail counter, Creeping counter, or Mobies counter.

• In n - bit Jhonson counter maximum used states = 2n, unused states = 2ⁿ - 2n.
• If the input clock frequency is f, the output frequency of each flip flop is f /2n and the duty cycle is 50%.
• A disadvantage of Jhonson Ring Counter: Lockout may occur. To decode each state one, two-input AND or NOR gate is used.