Circuit Theory : Kirchhoff's Laws

1. KIRCHOFF'S LAW

• Kirchhoff’s Voltage Law ( KVL): The sum of voltages around a closed loop circuit is equal to zero.
• Kirchhoff's Voltage Law (KVL) is Kirchhoff's second law that deals with the conservation of energy around a closed circuit path. ... This voltage law states that for a closed loop series path the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero.

• Kirchhoff’s Current Law ( KCL): The algebraic sum of electrical current that merge in a common node of a circuit is zero.
• Kirchhoff's Current Law (KCL) is Kirchhoff's first law that deals with the conservation of charge entering and leaving a junction. This idea by Kirchhoff is commonly known as the Conservation of Charge, as the current is conserved around the junction with no loss of current.

                                               ∑ I_IN = ∑I_OUT

2. STAR-DELTA TRANSFORMATION

• A part of a bigger circuit that is configured with the three-terminal network Y (or Δ) has to be converted into an equivalent Δ (or Y) through transformations.
• Applications of these transformations will be studied by solving the resistive circuits.

Delta (Δ) – Wye (Y) conversion:

Let us consider the network shown below and assumed the resistances ( R_AB, R_BC, R_CA) in Δ network are known. Now the requirement is to measure the resistance values of the branches of the Wye (Y) network that would produce same resistances when measured across similar pairs of terminals of Δ network. For this We have to write the equivalence resistance between any two terminals in the following form.

• on solving above equations, we get values for star network resistances 

Conversion from Wye or Star (Y) to Delta (Δ):

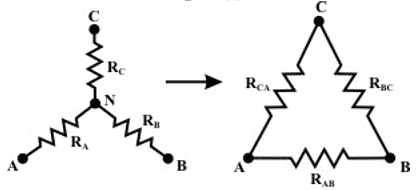
• To convert a Wye (Y ) to a Delta (Δ ), the relationships R_AB, R_BC & R₃ must be obtained in terms of the Wye (Y)  resistances R_A R_B and R_C Considering the Y connected network, we can write the current expression through R_A resistor as

• After equating the coefficients of V_AB and V_AC in both sides, we get the following relationship

• similarly we can obtain for R_BC for equivalent delta configuration

• Observations: With a view to the symmetry of the transformation equations, the Wye (Y) and Delta (Δ) networks have been superimposed on each other.
• The equivalent Wye (Y) resistance connected to a given terminal is equal to the product of the two Delta (Δ) resistances connected to that same terminal divided by the sum of all the Delta (Δ) resistances.
• The equivalent Delta (Δ) resistance between the two-terminals is the product of the two star (Y) resistances connected to those terminals divided by the third-star resistance plus the sum of the two same star (Wye) resistances.

You can avail of BYJU’S Exam Prep Online classroom program for all AE & JE Exams:

BYJU’S Exam Prep Online Classroom Program for AE & JE Exams (12+ Structured LIVE Courses)

You can avail of BYJU’S Exam Prep Test series specially designed for all AE & JE Exams:

BYJU’S Exam Prep Test Series AE & JE Get Unlimited Access to all (160+ Mock Tests)

Thanks

Team BYJU’S Exam Prep

Download  BYJU’S Exam Prep APP, for the best Exam Preparation, Free Mock tests, Live Classes.