STEP 1
Firstly, when you enter the exam hall, you need to write down the following master table in your rough sheet instantly (only the signs):-
NOTE: The above table should be entered before the exam starts, in rough sheet. Because, this will save time, and you can refer to it instantly later on.
STEP 2
Try solving the question instantly if possible, by checking whether + or - values can bring us to a conclusion.
See an example No. 1:-
x2 + 7x + 12 = 0
y2 - 5y + 6 = 0
The signs of X’s equation are + and +, which means their solution is - and -. Both are negative values. (Refer to the table)
The signs of Y’s equation are - and +, which means their solution values are + and +. Both are positive values.
Obviously, X’s possible values are both negative... And Y’s possible values are both positive.
Obviously, the solution is X < Y. We found out just by looking at the signs which will take hardly 5 seconds.
So, any question with signs as “+, +” and “-, +” can be instantly solved, (unless it's an unsolvable exception like x2 - 6x + 16 = 0, which can have no real integer as the answer. But this is a very rare occasion).
See another example, Example No. 2:-
x2 + 21x - 32 = 0
y2 + 7y - 12 = 0
The question’s signs are + and -, for both X & Y equations. This means X and Y’s values can be both positive or negative, as per the master table... The answer is an instant CND (Can Not Determine). This takes hardly 5 seconds.
Similarly, any question’s 2 equations with all 4 symbols as negative (-, -), will have each variable’s value either a positive or negative, so it's again a CND.
STEP 3
If you visit Step 3, it means the question is not instantly solved in Step 2. Here, we write the 2 possible signs of each variable anyways, like plus or minus, in our rough sheet.
We must find the possible values of the variables. Remember, from the 2 symbols (+ or -) derived from the master table, the first symbol connects to the bigger value, and the second symbol connects to the smaller value, numerically.
Example 3:-
x2 - 12x + 32 = 0
y2 - 7y + 12 = 0
The question’s symbols are -, + which means both values will be positive for each variable, x and y.
x2 - 4x - 8x + 32 = 0
X (x - 4) - 4 (x - 8) = 0
X = 4, X = 8
y2 - 7y + 12 = 0
y2 - 4y - 3y + 12 = 0
y (y - 4) - 3 (y - 4) = 0
Y= 4, Y = 4
So, X >= Y
This is a very basic example. Let’s move on to fractional example.
Example 4 is given below:-
2x2 + 3x - 9 = 0
2y2 - 11y + 15 = 0
+, - means X will be (-) or (+).
-, + means Y will be (+) or (+)
We have to solve it as we can’t decide instantly.
Now, due to a variation of a factor attached to squared values, the change in method is that we’ll have to multiply variable less value (9) with a factor of the squared variable (2), to get 18 for X’s equation.
We factorize 18 as 2 x 3 x 3 and reduce it to 2 values (which add/subtract to 3) which are 6 x 3... Now, divide both values by 2, because that is a factor of x2.
So, x = -6/2 or +3/2... In other words, x = -3 or 1.5.
Similarly for Y, we know the signs are + and -, which means both values are positive.
And 15 x 2 = 30. (Again, this is done because y2 has a multiplying factor of 2)
30 = 2 x 3 x 5. (we’ll have to multiply 2 values of these, to arrive at final 2 values which add upto 11, which are 6 and 5)
11 = 6 + 5. Now, Divide both 6 and 5 by 2 each, to get respective possible values of y.
So, x = -6/2, 5/2
y = 3 or 2.5.
STEP 4
Rank all the 4 values carefully, considering - as lower values and + as higher, as they normally are in mathematics.
For example,
“-5” will get rank 4,
“-0.8” will get rank 3,
“0.4” will get rank 2,
and “4” will get rank 1.
Write the ranks in your rough sheet, besides the values. Check the ranks and see what conclusion can be derived.
If there’s no tie up/ draw among the ranks, then the answer is easy to find...
So, as you can see from the table above, when all 4 values are different, and if the ranks 1 and 2 are together, they make it a senior variable, otherwise, we can’t determine and it becomes a CND.
When they are tied up, then we’ll have to work it out on rank to rank comparison basis to find a final solution, like below. But this we do only in mind:-
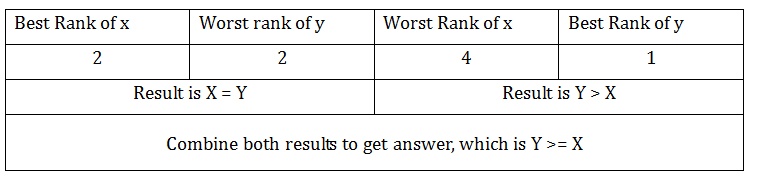
Let’s carry Example 3 from the Step 3 mentioned before...
X = -8, -4
Y = -4, -3
X’s ranks would be 4,2
Y’s ranks would be 2,1. (assuming that ranks 2 & 3 are combined to get rank 2)
We compare them by “Best vs Worst” method this way:-
If we ever have to combine a X>Y with X<Y, then its obviously CND. Rest you guys can figure out. Remember to do this Step 4 in mind itself, writing only the ranks on rough sheet and nothing else. Don’t make such tables there when the clock is running out...
Let’s solve Example 4 further from where we left:-
x = -6/2, 5/2
y = 3 or 2.5.
X’s ranks are= 4, 2
Y’s ranks are= 1, 2.
We compare best to worst and solve it in mind itself to get Y >= X.
Now let us check some special cases of inequality.
SPECIAL CASES:-
1. SQUARES - Let us take a few examples of non equation values. See example No. 5:-
x2 = 1600
y2 = 1600
The answer is CND. Because a square would always mean the possibility of a positive as well as a negative value,
x = 40, -40
y = 40, -40
Hence, any 2 squares or their variations are always CND, irrespective of the values.
NOTE: The root of a positive value is always positive. If you have to root a negative value, then the question is wrong, and hence, the answer is a CND.
See example No. 6:-
x2 - 243 = 468
y2 + 513 = 1023
Don’t touch the pen. It's a CND. Because, ultimately we’ll get a perfect/ imperfect square, which is always a CND.
2. LINEAR MIXED VARIABLE EQUATIONS
Example 7:-
5x + 4y = 82
4x + 2y = 64
One way to proceed is to equate either the “X” or “Y” part of both equations by multiplication any one equation with a positive integer.
Here, best way would be to double the second equation to form 8x + 4y = 128. We can now substract second equation from first,
8x + 4y = 128
- 5x + 4y = 82
------------------------
3x = 36
removing 4y from both sides easily to get X=12,
4y = 82 - 5x = 82 - 60 = 22,
y = 5.5,
There’s mostly no positive negative confusion in these cases. So, X > Y is right here.
==========================================





Comments
write a comment