In this article, you will find the study notes on Linear algebra which will cover the topics such as Matrix, Type of Matrix, Determinant of A matrix, Minors and Cofactors, Operation of A matrix, Properties of Matrices, Rank of Matrix, Eigenvalues and eigenvectors.
Matrix
A matrix is a rectangular array of numbers arranged in m horizontal rows and n vertical columns. The numbers are called entries of the matrix and such a matrix is said to have dimension m x n. Matrices are usually denoted by capital letters. A, B …….
A = [aij], i to m, j = 1 to n.

Type of Matrix
1.1 Row Matrix:
A matrix with only one row is called a row matrix.
e.g. = [ 1 2 4 ]1x3
1.2 Column Matrix:
A matrix with only one column is called a column matrix.
Eg: 1
2
3 3x1
1.3 Square Matrix:
A square matrix has an equal number of rows and columns. (i.e.) m = n.
Eg = 1 2 3
4 5 6
8 9 7 3x3
1.4 Diagonal Matrix:
A square matrix is called a diagonal matrix if each of its non-diagonal elements are zero (i.e.) A square matrix A is diagonal if aij ≠ 0 for i = j and
aij = 0 for i ≠ j.
Eg = 1 0 0
0 2 0
0 0 3 3x3
1.5 Diagonal Matrix:
A square matrix is called a diagonal matrix if each of its non-diagonal elements are zero (i.e.) A square matrix A is diagonal if aij ≠ 0 for i = j and
aij = 0 for i ≠ j.
Eg = 1 0 0
0 2 0
0 0 3 3x3
1.6 Scalar Matrix:
A diagonal matrix whose diagonal elements are equal is called a scalar matrix.
Eg = 4 0 0
0 4 0
0 0 4 3x3
1.7 Upper Triangular Matrix:
An upper triangular matrix is one whose entry values below the leading diagonal are zero.
Eg = 5 6 8
0 1 2
0 0 3 3x3
1.8 Lower Triangular Matrix:
A lower triangular matrix is one whose entry values above the leading diagonal are zeros.
Eg = 5 0 0
6 2 0
7 3 8 3x3
1.9 Equality of Matrices:
Two matrices are equal if they are of the same dimension and their corresponding entries are equal.
Eg: A = B
Where A = 1 2 B = 1 2
5 6 2x2 5 6 2x2
1.10 Transpose of a Matrix:
A matrix obtained from any given matrix A, by interchanging its rows and columns is called the transpose of A an dis usually denoted by A' (or) AT.
Thus if A = [aij], then A' = [bij] where bij = aij.
Eg: A = 1 2 A' = 1 4
4 5 2 5
1.11 Conjugate of A Matrix:
The matrix obtained from given matrix A, on replacing its elements by the corresponding conjugate complex numbers is called the conjugate of A and denoted by A. Thus if A = [aij], then A = [bij] where bij = aij is called the conjugate of A.
Eg: A = 1+2i 3-4i A' = 1-2i 3+4i
1-5i 2-6i 1+5i 2+6i
1.12 Conjugate transpose of A Matrix:
The conjugate of the transpose of a matrix A is called its conjugate transpose and denoted by A(H). Thus AT.
Eg: A = 1+2i 3-4i AT = 1-2i 1+5i
1-5i 2-6i 3+4i 2+6i
1.13 Symmetric Matrices:
A square matrix A = [aij] is said to be symmetric if aij = aji ,
(i.e.) the (i,j)th element is same as the (j, i)th element.
Eg: A = a h g = A' = a h g
h b f h b f
g f c g f c
therefore A = A'.
1.14 Skew-Symmetric Matrices:
A square matrix A = [aij] is said to be skew symmetric of aij = -aji.
(i.e.) the (i, j)th element is the negative of its (j, i)th element.
Eg: A = 0 a b A' = 0 -a -b
-a 0 c a 0 -c
-b -c 0 b c 0
therefore A = -A'.
1.15 Hermitian Matrices:
A square matrix A = [aij] is said to be Hermitian if aij = aji.
(i.e.) the (i, j)th elements is the conjugate complex of the (j, i)th elements.
(i.e.) for a Hermitian matrix A, we have A = A'.
1.16 Skew-Hermitian Matrices:
A square matrix A = [aij] is said to be skew-hermitian if aij = -aji.
(i.e.) the (i, j)th elements is the negative conjugate complex of the (j, i)th elements.
Eg: Hermitian matrices Skew-Hermitian Matrices
A = 1 2-3i A' = 1 2+3i
2+3i 0 2-3i 0
A' = 1 2+3i -A' = -1 -2-3i
2-3i 0 -2+3i 0
-A' = 1 2-3i
2-3i 0
2. Determinant of A matrix
If A = [aij] be a square matrix of order n, then the determinant of [aij] of order n, is called the determinant of the square matrix A, denoted by |A|
Eg:
A= 
|A| = 1(45-48) – 2(36-42) + 3(32-35)
= (-3) – 2(-6) + 3(-3)
= (-3) + 12 – 9
= -12 + 12
= 0.
IAI = 0.
2.1 Minors and Cofactors
The determinant of a square submatrix of a matrix is called a minor of A.
2.1.1 Minors:
The minor of an element in a determinant is the determinant got by suppressing the row and column in which the element appears. The order of the minor of an element in a determinant A is one less than the order of IAI. The minor of the element in the ith row. jth column is denoted by mij [The determinant of a square sub matrix of a matrix A is called a minor of A].
2.1.2 Cofactor:
The signed minor is called cofactor. The cofactor of the element in the ith row, jth column is denoted by cij and cij = (-1)i+j mij. The expansion of 3rd order determinant when expanded in terms of minors the sign of the cofactor of element will be as follows.

2.1.3 Adjoint or adjugate of a square matrix:
The adjoint or adjugate of a square matrix A is a transpose of the matrix formed by cofactors of elements of IAI Adjoint of matrix. A is denoted as adj A
adj A 
Note: If A is a non-singular square matrix then A(adj A) = (adj A) A = IAI I where I is unit matrix of same order as that of A.
2.1.4 Principle minor:
The principle minor of a matrix is the determinant of a square submatrix formed by deleting corresponding row and column vectors.
Eg: The principle minors of 3x3 matrix
adj A 
order 1 and

of order 2.
3. Operation of A matrix
3.1 Addition
- Order of the matrices must be the same
- Add corresponding elements together
- Matrix addition is commutative
- Matrix addition is associative
| A = |
| B = |
|
Both matrices have the same number of rows and columns (2 rows and 3 columns), so they can be added and subtracted. Thus,
| A + B = |
| A+ B= |
|
3.2 Subtraction
- The order of the matrices must be the same
- Subtract corresponding elements
- Matrix subtraction is not commutative (neither is subtraction of real numbers)
- Matrix subtraction is not associative (neither is subtraction of real numbers)
| A = |
| B = |
|
Both matrices have the same number of rows and columns (2 rows and 3 columns), so they can be added and subtracted. Thus, And,
| A - B = |
| A-B = |
|
3.3 Matrix Multiplication
Am×n × Bn×p = Cm×p
- The number of columns in the first matrix must be equal to the number of rows in the second matrix. That is, the inner dimensions must be the same.
- The order of the product is the number of rows in the first matrix by the number of columns in the second matrix. That is, the dimensions of the product are the outer dimensions.
- Since the number of columns in the first matrix is equal to the number of rows in the second matrix, you can pair up entries.
- Each element in row i from the first matrix is paired up with an element in column j from the second matrix.
- The element in row i, column j, of the product is formed by multiplying these paired elements and summing them.
- Each element in the product is the sum of the products of the elements from row i of the first matrix and column j of the second matrix.
- There will be n products which are summed for each element in the product.
Exmple:
Consider the product of a 2×3 matrix and a 3×4 matrix. The multiplication is defined because the inner dimensions (3) are the same. The product will be a 2×4 matrix, the outer dimensions.
![[[1,-2,3], [4,5,-2]] * [[1,-8,4,-3], [-3,6,7,2], [6,5,-1,4]]](https://grdp.co/cdn-cgi/image/width=500,height=500,quality=50,f=auto/https://people.richland.edu/james/lecture/m116/matrices/mult1.gif)
| Column 1 | Column 2 | Column 3 | Column 4 | ||
|---|---|---|---|---|---|
| values | [1, -3, 6] | [-8, 6, 5] | [4, 7, -1] | [-3, 2, 4] | |
| Row 1 | [1, -2, 3] | 1(1) - 2(-3) + 3(6) = 1 + 6 + 18 = 25 | 1(-8) -2(6) + 3(5) = -8 - 12 + 15 = -5 | 1(4) -2(7) +3(-1) = 4 - 14 - 3 = -13 | 1(-3) -2(2) + 3(4) = -3 -4 + 12 = 5 |
| Row 2 | [4, 5, -2] | 4(1) + 5(-3) -2(6) = 4 - 15 - 12 = -23 | 4(-8) + 5(6) - 2(5) = -32 + 30 - 10 = -12 | 4(4) + 5(7) -2(-1) = 16 + 35 + 2 = 53 | 4(-3) + 5(2) -2(4) = -12 + 10 - 8 = -10 |
So, the final product is
| 25 | -5 | -13 | 5 |
| -23 | -12 | 53 | -10 |
4. Properties of Matrices
| Property | Example |
|---|---|
| Commutativity of Addition | A + B = B + A |
| Associativity of Addition | A + ( B + C ) = ( A + B ) + C |
| Associativity of Scalar Multiplication | (cd) A = c (dA) |
| Scalar Identity | 1A = A(1) = A |
| Distributive | c (A + B) = cA + cB |
| Distributive | (c + d) A = cA + dA |
| Additive Identity | A + O = O + A = A |
| Associativity of Multiplication | A (BC) = (AB) C |
| Left Distributive | A (B + C) = AB + AC |
| Right Distributive | ( A + B ) C = AC + BC |
| Scalar Associativity / Commutativity | c (AB) = (cA) B = A (cB) = (AB) c |
| Multiplicative Identity | IA = AI = A |
1. Inverse of a Matrix
For a square matrix A, the inverse is written A-1. When A is multiplied by A-1 the result is the identity matrix I. Non-square matrices do not have inverses. Note: Not all square matrices have inverses. A square matrix which has an inverse is called invertible or nonsingular, and a square matrix without an inverse is called noninvertible or singular.
AA-1 = A-1A = I
Here are One ways to find the inverse of a matrix:
|
2. Rank of a Matrix
The maximum number of linearly independent rows in a matrix A is called the row rank of A, and the maximum number of linearly independent columns in A is called the column rank of A. If A is an m by n matrix, that is, if A has m rows and n columns, then it is obvious that
![]()
Example 1: Find the rank of the matrix

First, because the matrix is 4 x 3, its rank can be no greater than 3. Therefore, at least one of the four rows will become a row of zeros. Perform the following row operations:

Since there are 3 nonzero rows remaining in this echelon form of B, ![]()
3. Eigen values and eigen vectors
A = [aij] be a square matrix of order n. if there exists a non-zero column vector X and a scalar l such that AX = lX, then l is called Eigen value of the matrix A and X is called an Eigen vector corresponding to the eigen value l.
Characteristic Matrix:
The matrix A – lI is called characteristic matrix of given matrix A which is obtained by subtracting l from diagonal elements of A.
Characteristic Polynomial:
The determinant IA – lII when expanded will give a polynomial of degree n in l which is called characteristic polynomial of matrix A.
Characteristic equation:
The equation IA - lII = 0 is called characteristic equation or secular equation of matrix A.
Characteristic Roots or Eigen values or Latent roots:
The roots of the characteristic eq. l1, l2 ……… ln are called characteristic roots or Eigen values or Latent roots.
Characteristic Vectors or Eigen Vectors:
Corresponding to each characteristic root l there corresponds non-zero vector X satisfying the equation (A - lI) X = 0. The non-zero vectors X are called characteristic vectors or Eigen vectors.
Spectrum of a Matrix:
The set of all Eigen values of given matrix A is called the spectrum of A
Example :
Example: Find Eigenvalues and Eigenvectors of a 2x2 Matrix
If

then the characteristic equation is

and the two eigenvalues are
λ1=-1, λ2=-2
All that's left is to find the two eigenvectors. Let's find the eigenvector, v1, associated with the eigenvalue, λ1=-1, first.

so clearly from the top row of the equations, we get
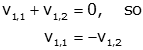
Note that if we took the second row we would get

In either case we find that the first eigenvector is any 2 element column vector in which the two elements have equal magnitude and opposite sign.

where k1 is an arbitrary constant. Note that we didn't have to use +1 and -1, we could have used any two quantities of equal magnitude and opposite sign.
Going through the same procedure for the second eigenvalue:

Again, the choice of +1 and -2 for the eigenvector was arbitrary;
Thanks,
Team Gradeup






Comments
write a comment