In this article, we will discuss the Circles and various theorem related to it. The circle is the most important topic of Geometry. In this article, I have covers tangents, chords and some important short trick also.
CIRCLE:
- A circle is a set of point or locus of a point which are at a fixed distance from a point called as a centre.
- The distance of any point on the circumference of the circle from the centre of the circle is equal.
Diameter:
Diameter is double of the radius .i.e. D=2R.
Diameter is the chord which passes through the centre of the circle.
Tangent: A line which touch the circle at only one point at its circumference.
Secant: A line which touch the circle at two distinct points.
Chord: A line Segment which lie inside the circle and its end points are always lie on the circle.
Important theorem and results of the circle:
(1) Of the two chords of the circles, the one which is greater is nearer to the centre.
(2) The perpendicular from the centre of the circle bisect the chord i.e. radius always bisect the chord if perpendicular
(3) Any line segment joining the centre of the circle and the mid point of the chord is perpendicular to the chord.
If AM=MB then OM is perpendicular to the AB.(reference to above fogure)
(4)Equal chord of the circle always subtends the equal angles at the centre of the circle.
i.e. if AB=CD then ∠1=∠2
(5) If angle subtended by the two chord at the centre are equal then the chords are always equal.
(3) Equal chords of the circle are at equal distance from the centre.
(6) Chords which are at equidistant from the centre of the circle are always equal.
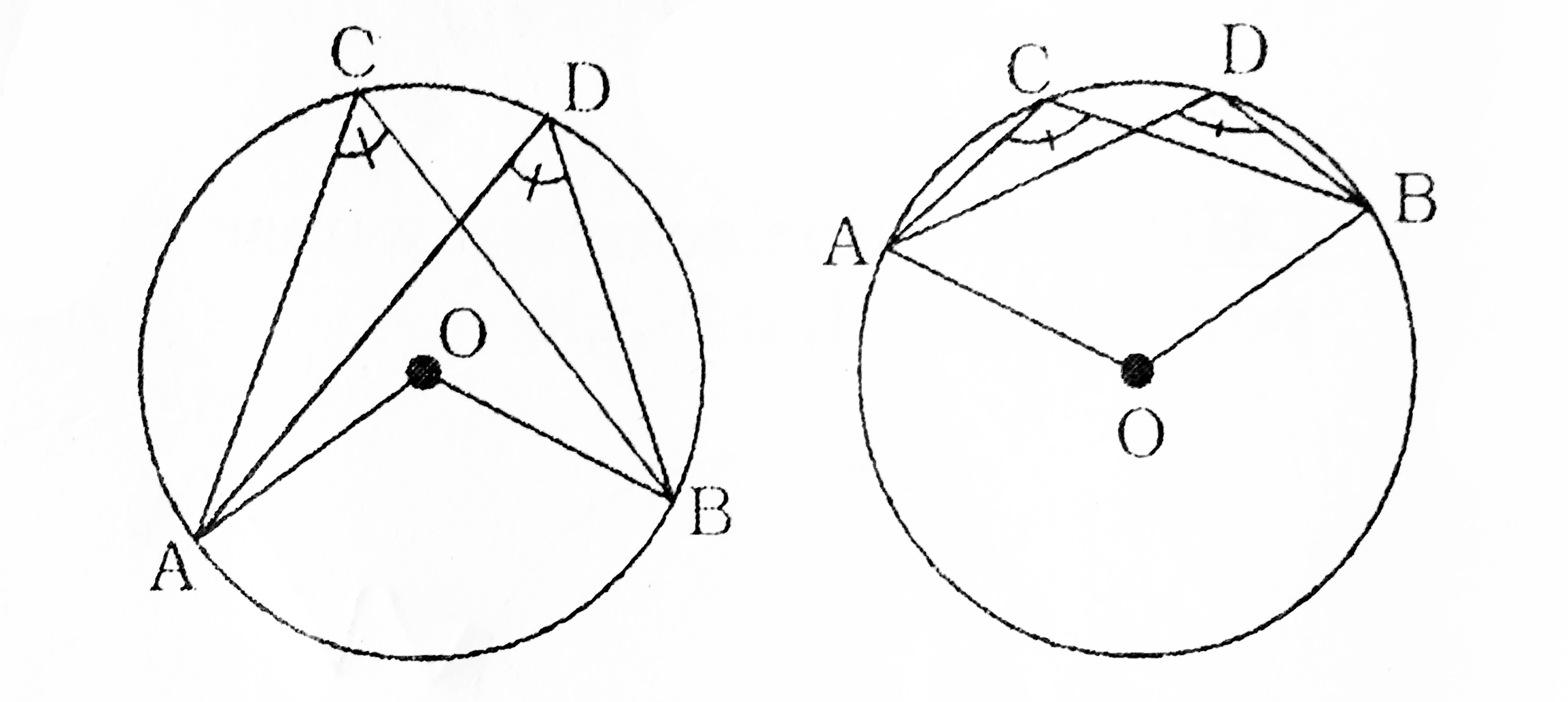
(7) Angle subtended by any arc at the centre of the circle is double the angle subtended by it at any point on the remaining part of the circle.
∠x=2∠y
(8) Angle subtended by an arc in the same segment of the circle are equal.
∠ACB=∠ADB
(9) Angle in a semi circle is a right angle. i.e the angle subtended by the diameter is always right angle.
(10) The circle drawn with hypotenuse of a right angle triangle as diameter, passes through its opposite vertex.
(11) The sum of the opposite angle of a cyclic quadrilateral is always 180°.
Cyclic quadrilateral is that quadrilateral whose all point lie on the circumference of the circle.
∠A+∠C=∠B+∠D
(12) If a side of a cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.
∠1=∠2
Some important points of tangents
(1)Tangent and radius always make the angle of 90 at the point of meeting of tangent with the circle.
If AB is a tangent at P, then OP is perpendicular to AB.
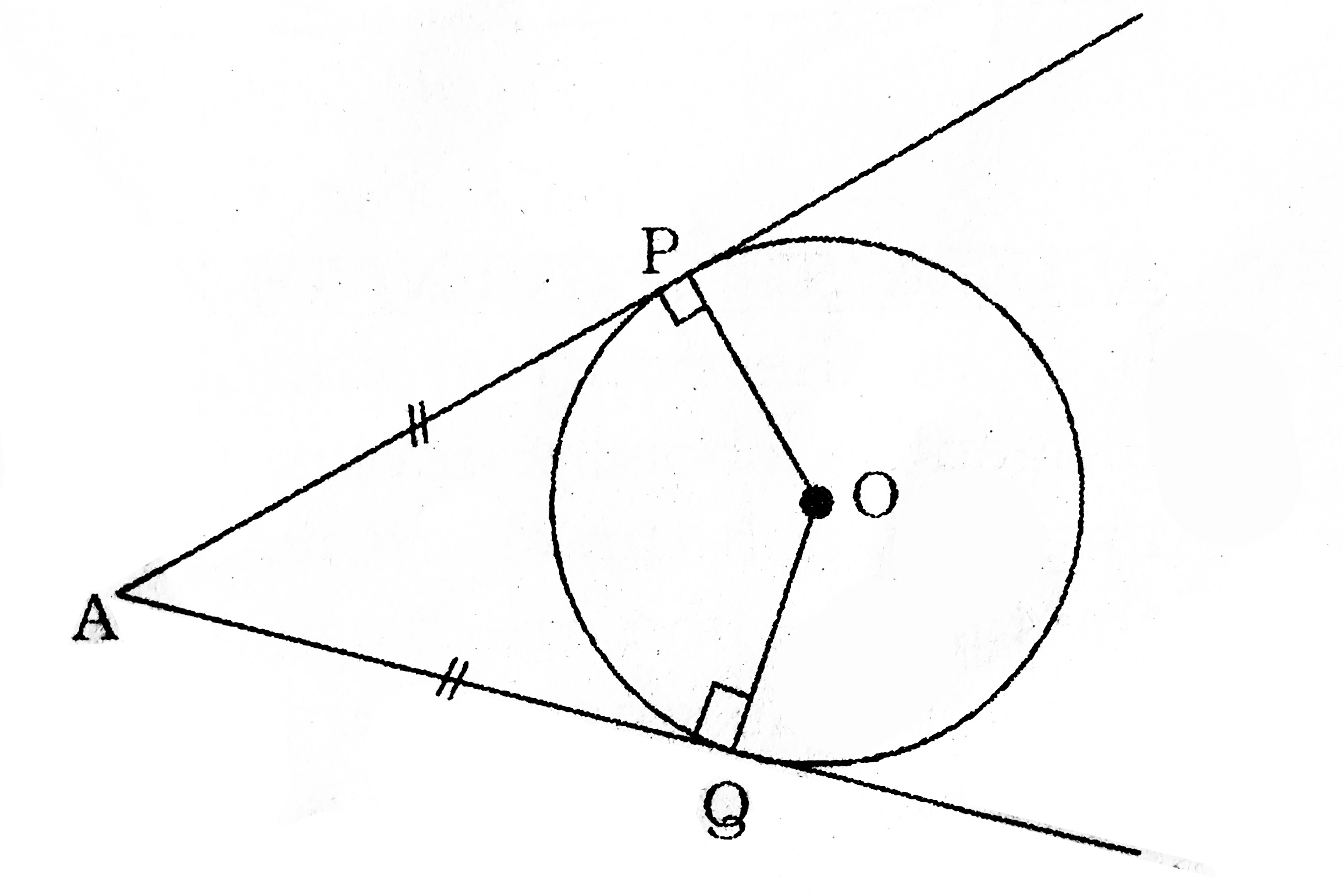
(2) The length of the two tangent drawn from the same external point to a circle is always equal.
AP=AQ
(3) If two chords AB and CD intersect internally or externally at point P then.
PA*PB=PC*PD
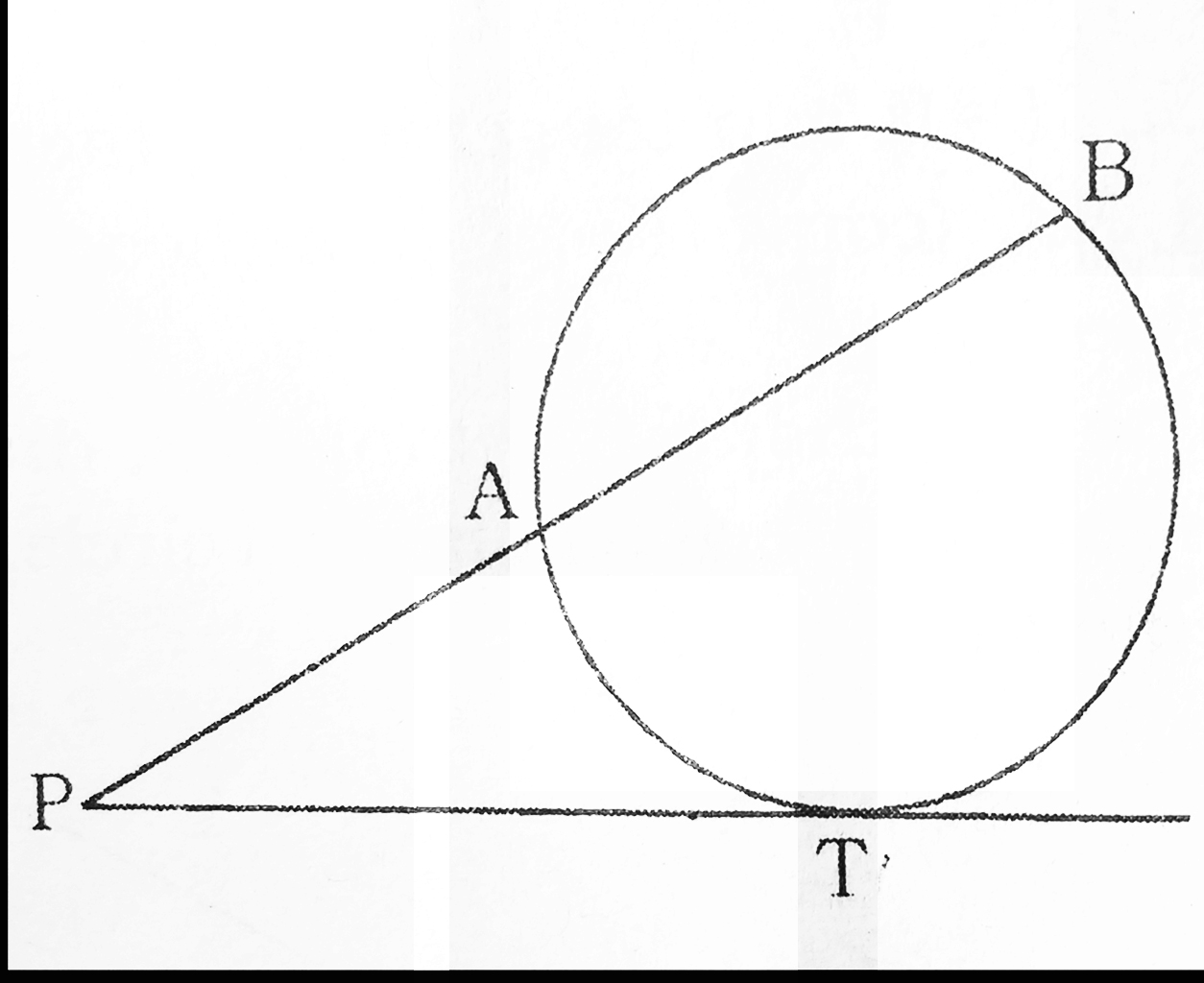
(4) If PAB is a secant which intersects the circle at A and B and PT be a tangent at T, then
PT2=PA*PB
(5) If from the point of contact of tangent with circle, a chord is drawn ,then the angles which the chord makes with the tangent line are equal respectively to the angles formed in the corresponding alternate segment.
∠BAT=∠BCA=∠1
∠BAP=∠BDA=∠2
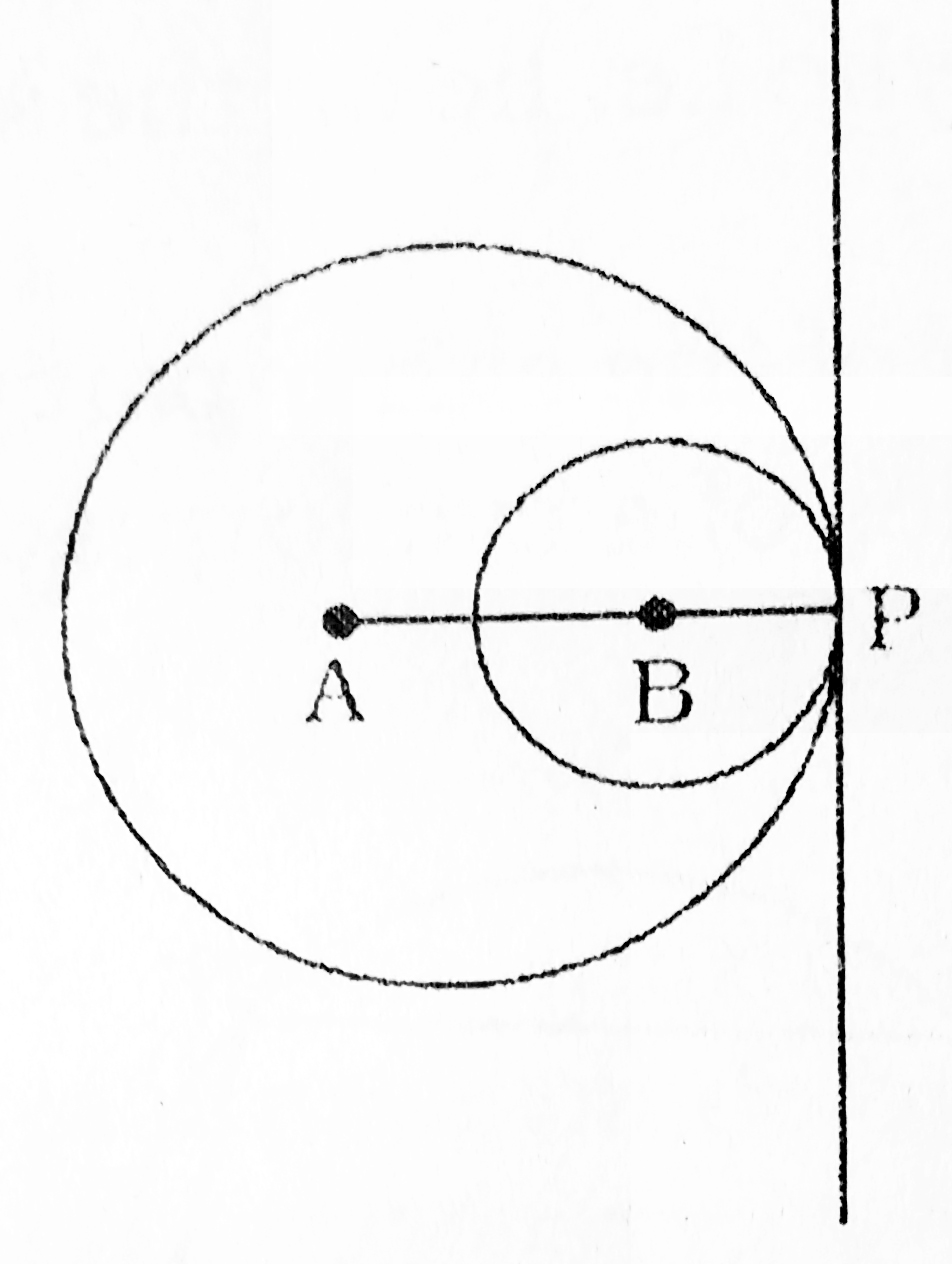
(6) If two circles touch each other internally or externally the point of contacts lies on the line joining their centres.
Distance between the cntres
When touch internally, distance=AP-BP
When touch externally, distance =AP+BP
Some Important Results:
(1)If two tangent PA and PB are drawn from the external point P, then
∠1=∠2 and ∠3=∠4
OP is perpendicular to AB and AC=BC
(2) r1 and r2 are the radius of two circles and d is the distance between the centres of the circle then the length of the common tangent of two circles is given by
(3) If r1 and r2 are the two radius of the circle and "d" is the distance between them then the length of the transverse common tangent is given by

(4) If a circle touches all the four sides of a quadrilateral then the sum of opposite pair of sides are equal.
i.e. AB+CD=AD+BC
(5) If two chords AB and AC of a circle are equal then the bisector of ∠BAC passes through the centre O of the cirlcle.
(6) The equilateral formed by the angle bisector of a cyclic quadrilateral is also cyclic.
(7) If a cyclic trapezium is isosceles then its diagonals are equal
i.e if AB parallel DC and AD=BC then AC=BD
(8) Angle in the major segment of a circle is acute and angle in minor segment is obtuse.
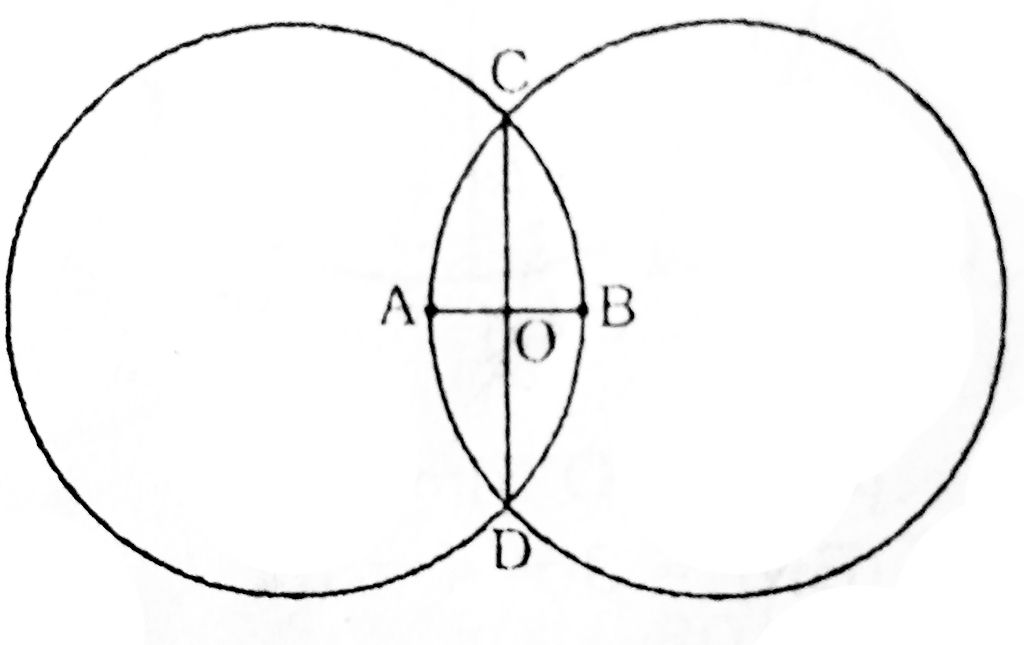
(9) If two circles of same radius r are such that the centre of one lies on the circumference of the other then the length of the common chord is given by l=√3*r
(10) If 2a and 2b are length of two chords which intersects at right angle and if the distance between the centre of the circle and intersecting point of the chords is C then the radius of circle is given by]
![]()
(11) If three circles of radius r are bound by a rubber band then the length of rubber band is given by
6r+2πr
Click Here to Know about Online Classroom Program!
More from us:
Important Study Notes for Defence Exams
Thanks
The Most Comprehensive Exam Prep App





















Comments
write a comment