In this article, you will find the Study Notes on Electric Flux Intensity which will cover the topics such as Electric Field due to Infinite Line Charge, Electric Field due to Uniformly Charged Ring, Electric Field due to Infinite Sheet of Charge and Superposition Principle of Fields.
Force per unit charge is called electric field intensity
![]()
![]() line charge
line charge
Where, ρL is line charge density in C/m and r is radial distance.
![]() surface charge
surface charge
Where, ρS is surface charge density in C/m2 and an is unit vector normal to the plane containing the sheet.
Electric Field due to Infinite Line Charge
Consider an infinitely long straight line carrying uniformly line charge having density ρL C/m. The electric field intensity at point P.

![]() volt/metre
volt/metre
Electric Field due to Uniformly Charged Ring
Consider a charged circular ring of radius r placed in XY plane with centre at origin. Carrying a charge uniformly along its circumference. The charge density is ρL C/m.
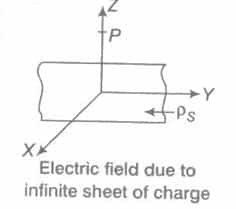
Electric Field due to Infinite Sheet of Charge
Consider an infinite sheet of charge having uniform surface charge density ρs C/m2, placed in XY plane. We want to find E at point P present at Z-axis.
![]() volt/metre
volt/metre
Superposition Principle of Fields
The electric field of a point charge is a linear function of the value of the charge. The fields of more than one point charge are linearly superimposable by vector addition. This is the principle of superposition applied to electric field and states that the total resultant field at a point is the vector sum of the individual components of field at the point.





Comments
write a comment