What is Topological Sort?
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Topological Sort exists if and only if the graph does not contain any cycle (that is, no self-contradict constraints). These precedence constraints form the directed acyclic graph. Any topological sort (also known as the linear extension) defines an order to do these tasks such that each is performed only after all of its constraints are satisfied.
Suppose we have a set of tasks, but specific tasks must be performed before others. Only one task can be performed at a time, and each must be completed before the next task begins. Such a relationship can be represented as a directed graph, and topological sort can be used to schedule tasks under precedence constraints. We will determine if an order exists such that this set of tasks can be completed under the given constraints. Such an order is called a topological sort of graph G, where G is the graph containing all tasks, the vertices are tasks, and the edges are constraints. Here, we will discuss the definition of topological sort and various topological sorting methods.
Download Formulas for GATE Computer Science Engineering – Programming & Data Structures
Table of content
Definition of Topological Sort
The topological sort of a DAG G(V, E) is a linear ordering of all its vertices such that if G contains an edge (u, v), then u appears before v in the ordering.
Mathematically, this ordering is described by a function t that maps each vertex to a number
t: V → (1, 2,…, n): t(v) i such that t(u) < t(v) < t(w) for the vertices u, v, w of the following diagram:
In the above diagram, we see that the node u has no incoming edge, and u comes first as above said, so the node u is removed and added to the topological sort order as u now the node v comes, it also not has incoming edges so, node v is removed and update the topological sort order as uv. Similarly, for the last node, the topological sort order is uvw.
Download Formulas for GATE Computer Science Engineering – Algorithms
Topological Sort using DFS
The topological sort time complexity using DFS takes θ(m+n) time, and the insertion of each vertex to the linked list takes O(1) time. Thus, topological sort using DFS takes time θ(m + n). The following algorithm is as follows:
1. Perform DFS to compute finishing times f[v] for each vertex v
2. As each vertex is finished, insert it to the front of a linked list
3. Return the linked list of vertices
Topological Sort using Bucket Sorting
This algorithm computes a topological sort of a DAG beginning from a source and uses bucket sorting to arrange G nodes by their in-degree (# incoming edges).
An array of lists of nodes forms the bucket structure. Each node also maintains links to the vertices (nodes) to which its outgoing edges lead. The lists are sorted so that all vertices with n incoming edges lay on the list at the nth position of the table, as shown in the figure:
Download Formulas for GATE Computer Science Engineering – Discrete Mathematics
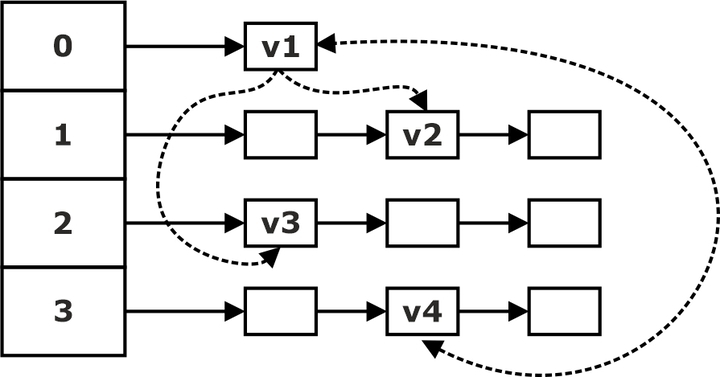
The main idea is to exclude a node that does not depend on any other at each step. That maps to removing an entry v1 from the 0th index of the bucket structure (which contains the sources of G) and reducing by one the in-degree of the entry’s adjacent nodes and reallocating them in the bucket. This means that node v2 is moved to the list at the 0th index and thus becomes a source. v3 is moved to the list at the 1st index, and v4 is moved to the list at the 2nd index. After subtracting the source from the graph, new sources may appear because the source edges are excluded from the graph, or there is more than one source. Thus the algorithm subtracts a source at every step and inserts it into a list until no sources (and consequently no nodes) exist. The resulting list represents the topological sort of the graph.



