Binary Search Tree
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Binary Search Tree is the advanced algorithm for analyzing the node and its left and right branches, which are modeled in a tree structure and return the value. A binary search tree, also known as an ordered or sorted binary tree in computer science, is a rooted binary tree data structure whose internal nodes each hold a key that is higher than all the keys in the node’s left subtree but less than those in the node’s right subtree.
The Binary Search Tree (BST) is devised on the architecture of the basic binary search algorithm. Hence it enables faster lookups, insertions, and removals of nodes. Further, in the upcoming sections, we will discuss the time complexity of binary search trees, data structure, abstract data type, and a lot more.
Download Formulas for GATE Computer Science Engineering – Programming & Data Structures
Table of content
-
1.
What is a Binary Search Tree?
-
2.
What is an ADT for a Binary Search Tree?
-
3.
Data Structure of a Binary Search Tree
-
4.
What is a Skew Binary Search Tree?
-
5.
Searching the Tree
-
6.
How to Find Minimum and Maximum in a Binary Search Tree?
-
7.
Successor in Binary Search Tree
-
8.
Important Binary Search Tree Topics for GATE CS
-
9.
Tips to Solve Binary Search Tree Questions in GATE CS
-
10.
Importance of Binary Search Tree in GATE
-
11.
Most Recommended Books for Binary Search Tree
What is a Binary Search Tree?
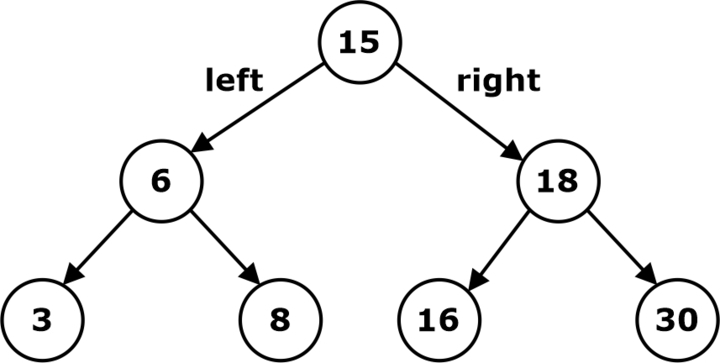
A binary search tree (BST) is the binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node’s left subtree and smaller than the keys in all nodes in that node’s right subtree.
- Node x
- Data in Left(x) is less than x
- Data in Right(x) is greater than x
- Notation: Key(x) means the data is in Node x.
Expression Trees
(a) (a + (b×c)) + (((d×e) + f)×g)
(b) General evaluation strategy: inorder traversal
Left, Op, Right
(c) Postorder:
Left, Right, Op
(d) Preorder:
Op, Left, Right
What is an ADT for a Binary Search Tree?
BST(Binary Search Tree) as Abstract Data Type. Many functions are as follows:
- Insert(x) // Insert item
- Find(x) // find item
- Delete(x) // delete item
- Traverse() // visit nodes in tree (several different ways)
- Minimum() // find minimum
- Maximum() // find maximum
- Successor(x) // find x’s successor
Download Formulas for GATE Computer Science Engineering – Discrete Mathematics
Data Structure of a Binary Search Tree
The data structure and pseudocode of the binary search tree are as follows
struct Node
{
int data;
Node*left;
Node*right;
};
Keep a pointer called
oot to the tree.
All you need to maintain is a node root to access any nodes in the tree!
This is like a linked list. Remember, for the linked list; we only need to store the head pointer.
Reminds you of a linked list? Remember, X = X → next;
Now we have:
if(x → left)
x= x → left: (more to left)
if(x → right)
x= x → right: (more to right)
Download Formulas for GATE Computer Science Engineering – Algorithms
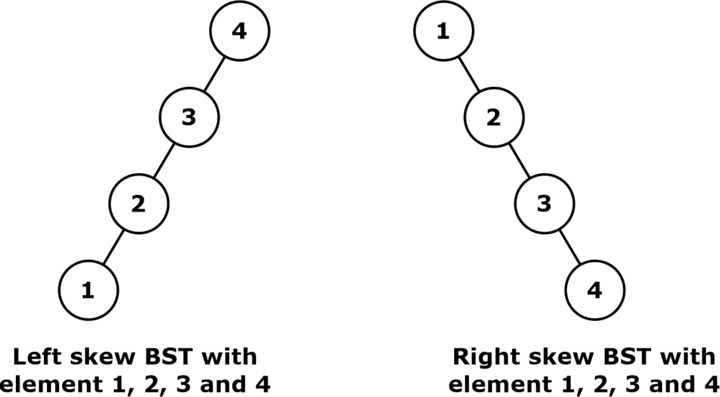
What is a Skew Binary Search Tree?
When the height of a BST goes till ‘n’ with ‘n’ elements, the tree is said to be skew BST. There are two types of skew binary search trees:
1. Left skewed BST
2. Right skewed BST
Searching the Tree
The pseudocode of the binary search tree is as follows:
Search(x, k)
Check if k is in the Tree.
Algorithm Search(x, k)
Input: x is the tree’s root, and k is the input search key.
Output the node containing k or NULL
1. while x ≠ NULL
2. do if k = key(x)
3. then return x;
2. else
5. if k < key(x)
6. then x:= left(x);
7. else x:=right(z);
8. return NULL;
Running time = O(tree height)
Example: Search(root 17)
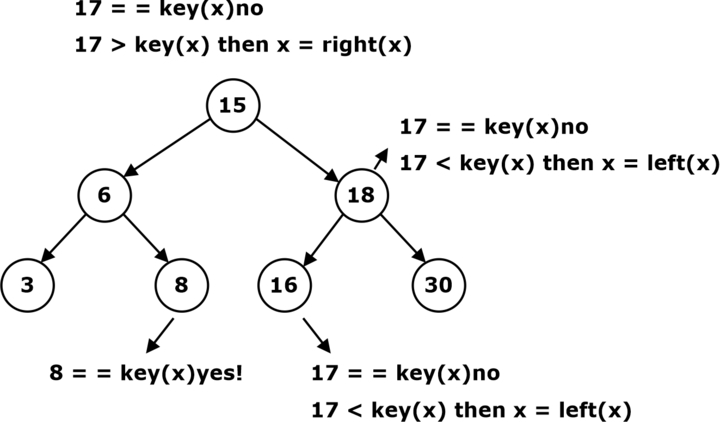
X==NULL
Stop… Not found.
How to Find Minimum and Maximum in a Binary Search Tree?
The leftmost node of the BST(binary search tree) is always the minimum element. The rightmost node of the BST(binary search tree) is always the maximum element. The time complexity of the worst case is the height of the tree.
Algorithm Minimum(x)
Input: x is the root
Output: the node containing the minimum key
1. while left(z) ≠ NULL
2. do x:=left(z)
3. return x;
Algorithm Maximum(x)
Input: x is the root
Output: the node containing the maximum key.
1. while right (x) ≠ NULL
2. do x:=right (x)
3. return x;
Successor in Binary Search Tree
The successor of node x in a binary search tree is node y, whose key(y) is the successor of key(x) in sorted order of the tree.
Three Scenarios to Determine Successors:
Scenario-1:
- Node x has the right subtree.
- By definition of BST(binary search tree), all items greater than x are in this right sub-tree.
- The successor is the minimum (right(x)).
Scenario-2:
- Node has no right subtree,
- X is the left child of the parent(X).
- The successor is the parent(X)
- The successor is a node whose key would appear in the next sorted order. Think about in order traversal.
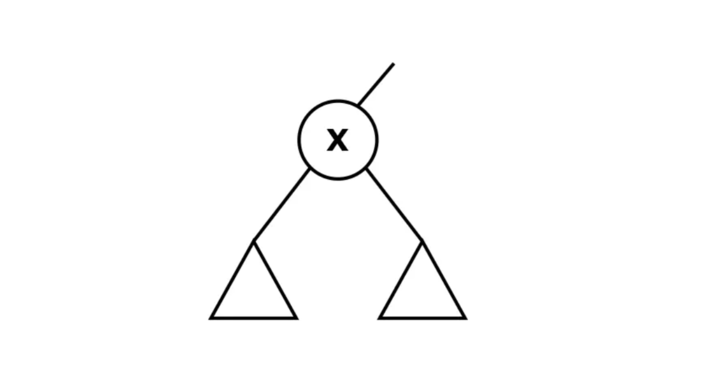
Scenario-3:
Node x is not a left child of the immediate parent.
Keep moving up the tree until you find the parent, which branches from the left().
Must traverse up the tree until we find a suitable parent
As stated in Pseudocode:
y parent (x);
while y ≠ NULL and x=right (y)
do x:=y:
x-parent (y);
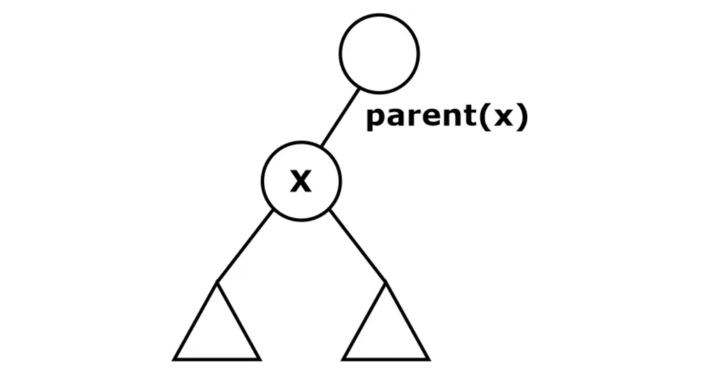
Algorithm Successor(x)
Input: x is the input node.
1. if right (x) ≠ NULL
2. then return Minimum (right (x)); [Scenario-1]
3. else
4. y:=parent (x);
5. while y ≠ NULL and x-right (y)
6. do x:=y; (Scenario-2 and 3)
7. y:=parent (y);
8. return y;
Successor (r, x)
Input: r is the tree’s root, and x is the node.
1. initialize an empty stack S;
2. while key (r) #key (x)
3. do push(s, r);
4. if key (x) < key (r)
5. then r:=left (r);
6. else r:=right (r);
7. if right (x) ≠ NULL
8. then return Minimum (right (x));
9. else
10. if s is empty
11. then return NULL;
12. else
13. y:=pop (S);
14. while y# NULL and x=right (y)
15. do x:=Y ;
16. if s is empty
17. then y:=NULL;
18. else y:=pop (S);
19. return Y;
Important Binary Search Tree Topics for GATE CS
The data structure is a broad subject topic and has a vast syllabus. The major topics for binary search tree study material for GATE CS are below.
|
Topic |
Explanation |
|
Checking and Searching |
You can perform various checking and searching operations in the binary search tree. Examples include finding the n^th largest element or the extra space in the BST. |
|
Red Black Tree and Threaded binary tree |
It includes the subtype of binary trees that are threaded and red-black binary trees. |
|
BST Operations |
Various operations other than searching can be performed on the binary search tree. |
Tips to Solve Binary Search Tree Questions in GATE CS
You can follow the following tips while solving binary search tree questions. Prepare for the topic by solving last year’s question papers well.
- Binary search trees GATE questions and answers PDF are based on the binary search tree and their uses in different scenarios. Hence you should focus on the data structure section for programming topics.
- Prepare excellent binary search tree notes containing all the syntactic analysis details for the GATE. Those binary search tree GATE notes will help you in revisions.
- Practice on binary search tree online quiz from online sites. These online tests help you in preparation for the real exam.
- Be clear with the binary search tree topics for GATE CS as many repetitive topics, such as transforming BST into the greater sum or finding the n^th largest element.
Importance of Binary Search Tree in GATE
The binary search tree is integral to the GATE and other competitive exams. Its importance is explained below:
- It checks whether you can make a binary tree and perform various functions. It also checks your grasp of the binary search tree GATE syllabus.
- The weightage of this topic is 2% to 5% in the exam.
- GATE requires you to acquire a basic knowledge of data structures and algorithms. It helps to maintain the accuracy of any main program.
- These concepts are useful in real-life situations as software engineers and/or data analysts solve various data structure problems.
Most Recommended Books for Binary Search Tree
The following are some excellent books on binary search tree for computer science that can help you prepare for the GATE exam.
|
Book Title |
Author |
|
Binary Search Tree |
Russell Jesse |
|
Adaptive Binary Search Tree |
Jonathan C. Derryberry |
|
On Some Hash Functions: Constructing a randomized binary search tree and a hash table |
Roger Doss |
|
Important GATE Topics |
|
| Fixed End Moment | Gravity Of Earth |
| Slope Deflection Equation | Capacitors in Parallel |
| Capacitors in Series | Carnot Cycle |
| Cement Test | Clamping Circuit |
| CMOS Converter | Column Base |


